7.9 KiB
Проверка статистических гипотез¶
Задача: есть некоторое статистическое утверждение (гипотеза) $H$ и есть набор экспериментальных данных $X$. Требуется сделать утверждение о степени достоверности гипотезы H при заданном наборе $X$.
В большинстве случаев речь идет о проверке единственной гипотезы, которую принято называть нулевой $H_0$. В отдельных случаях стоит также задача выбора наиболее подходящей гипотезы из набора $H_0,~H_1,~H_2,~...$
Для формализации процесса проверки гипотезы требуется ввести ФПВ: $f(X|H_0)$, характеризующее вероятность получить заданные наблюдаемые результаты в случае, если гипотеза верна.
Замечание Вообще говоря, уже этого распределеня достаточно для того, чтобы понять, верна гипотеза или нет. Если вероятность получить набор данных велика, то гипотеза наверное не верна. С другой стороны, возникает проблема с тем, что сложно понять, на сколько именно (с какой достоверностью) верна или не верна гипотеза нормировки распределений часто вычисляются не верно.
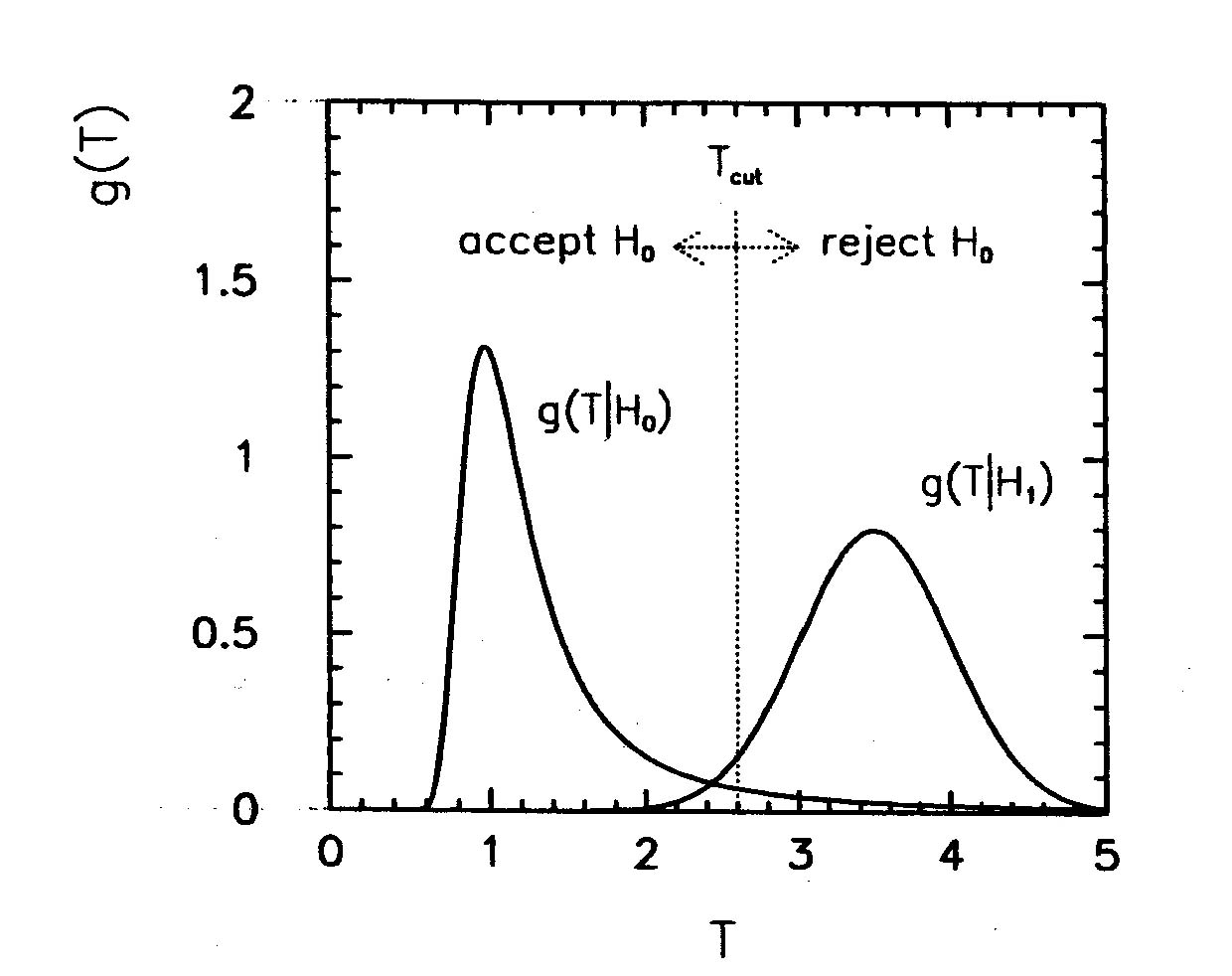
Для упрощения процесс принятия решения, используют функцию, называемую проверочной статистикой: $T(X)$, где T - число. Для такой статистики довольно легко построит ФПВ: $g(T|H_0)$.
Для критерия $T$ вводится понятие критического значения или критической области $T_0$. В случае, если значение $T$ превышает критическое значение (или выходит из критической области), то гипотеза считается не верной. Если значение в области, гипотеза считается верной.
Величина $$ \alpha = \int_{T_0}^\inf {g(T|H_0)} $$ показывает вероятность ошибки I рода. То есть вероятность отвергнуть гипотезу, когда она верна. Величину $1-\alpha$ называют уровнем достоверности критерия.
В случае, если существует единственная альтернативная (исключающая $H_0$) гипотеза $H_1$, то также можно определить величину ошибки II рода, то есть вероятность принять $H_0$ в случае если она не верна: $$ \beta = \int_{-\inf}^{T_0} {g(T|H_1)} $$
Величину $1-\beta$ называют мощностью критерия при заданной достоверности $1-\alpha$.
Среди двух критериев предпочтительным является тот, для которого мощность при той же значимости выше. Критерий, который будет более мощным для всех возможных состояний природы, называют равномерно более мощным критерием.
Построение критической области критерия¶
Визуально подбро критической области критерия можно сделать следующим образом:
- Берем распределение $g(T|H_0)$.
- Интегрируем его и получаем интегральное распределение: $G(T|H_0) = \int{g(T|H_0)}$. При необходимости перенормируем в диапазон [0,1].
- Проводим линию на уровне нужного уровня значимости (например C. L. 95%).
- Пересечение этой линии с графиком проектируется на ось T и это значение и будет означать критическую область.
Качество фита (стандартные критерии)¶
Критерий Пирсона¶
Проверочная статистика: $$ \chi^2 = \sum{\frac{ (O_i-E_i)^2}{E_i}} $$
Асимпототически приближается к $\chi^2$ распределению.
Критерий соотношения правдоподобия¶
Пусть $\Theta$ - пространство параметров $\theta$, а $\Omega*$ - область пространства парамеров, на принадлежность которой мы хотим проверить данные. В качестве проверочной статиситки выбирается: $$ \lambda = \frac{L(X|\theta \in \Omega)}{L(X|\theta \in \Theta)} $$
Величина $-2ln\lambda$ распределена как $\chi^2(r)$, где r - количество фиксированных параметров в $\Omega$
Сложные гипотезы¶
Положим что есть семейство гипотез $H_i$, среди которых надо выбрать наиболее достоверную. Выбор можно сделать двумя способами:
- Выбираем ту гипотезу, для которой $g(T|H_i)$ максимален.
- Выбираем ту гипотезу, для которой $\int_T^\inf{g(T|H_i)}$ максимален.
Если принять $T = L(X|\theta)$, то решение по первому методу сводится к методу максимуму правдоподобия.