Update materials 2021
This commit is contained in:
parent
52a85f99a4
commit
498892780f
.gitignore
notebooks/python
Теория вероятности
Теория оценок
Теория решений
1
.gitignore
vendored
1
.gitignore
vendored
@ -1 +1,2 @@
|
|||||||
.ipynb_checkpoints/
|
.ipynb_checkpoints/
|
||||||
|
.idea/
|
||||||
File diff suppressed because one or more lines are too long
File diff suppressed because one or more lines are too long
893
notebooks/python/fitting.ipynb
Normal file
893
notebooks/python/fitting.ipynb
Normal file
@ -0,0 +1,893 @@
|
|||||||
|
{
|
||||||
|
"cells": [
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "slide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"# Общий случай"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"## Постановка задачи"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "fragment"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"Пусть есть параметрическая модель $M\\left( \\theta \\right)$, где $\\theta$ - параметры."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "fragment"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"Функция правдоподобия $L\\left( X | M\\left( \\theta \\right) \\right)$ определят достоверность получения набора данных $X$ при заданном наборе параметров и данной модели."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "fragment"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"**Задача**: определить такой набор параметров $\\theta$, для которого функция принимает наибольшее значение."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"## Классификация\n",
|
||||||
|
"\n",
|
||||||
|
"По порядку производной:\n",
|
||||||
|
"\n",
|
||||||
|
"* Не использует производных $L$\n",
|
||||||
|
"\n",
|
||||||
|
"* Использует первую производную $\\frac{\\partial L}{\\partial \\theta_i}$ (градиент)\n",
|
||||||
|
"\n",
|
||||||
|
"* Использует вторые прозиводные $\\frac{\\partial^2 L}{\\partial \\theta_i \\partial \\theta_j}$ (гессиан)"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "slide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"## Без производных"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"### Прямой перебор\n",
|
||||||
|
"(brute force)\n",
|
||||||
|
"* Строим сетку и ищем на ней максимум. \n",
|
||||||
|
"* Возможен только для одномерных, максимум двумерных задач. \n",
|
||||||
|
"* Точность ограничена размером ячкйки сетки."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "fragment"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"### Симплекс методы \n",
|
||||||
|
"1. Строим многоугольник в пространстве параметров с $n+1$ вершинами, где $n$ - размерность пространства. \n",
|
||||||
|
"2. Орпделеляем значения функции в каждой вершине. \n",
|
||||||
|
"3. Находим вершину с наименьшим значением и двигаем ее к центру масс многоугольника."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
""
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "code",
|
||||||
|
"execution_count": 1,
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"outputs": [
|
||||||
|
{
|
||||||
|
"name": "stdout",
|
||||||
|
"output_type": "stream",
|
||||||
|
"text": [
|
||||||
|
"Optimization terminated successfully.\n",
|
||||||
|
" Current function value: 0.000000\n",
|
||||||
|
" Iterations: 339\n",
|
||||||
|
" Function evaluations: 571\n"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"data": {
|
||||||
|
"text/plain": [
|
||||||
|
" final_simplex: (array([[1. , 1. , 1. , 1. , 1. ],\n",
|
||||||
|
" [1. , 1. , 1. , 1. , 1. ],\n",
|
||||||
|
" [1. , 1. , 1. , 1.00000001, 1.00000001],\n",
|
||||||
|
" [1. , 1. , 1. , 1. , 1. ],\n",
|
||||||
|
" [1. , 1. , 1. , 1. , 1. ],\n",
|
||||||
|
" [1. , 1. , 1. , 1. , 0.99999999]]), array([4.86115343e-17, 7.65182843e-17, 8.11395684e-17, 8.63263255e-17,\n",
|
||||||
|
" 8.64080682e-17, 2.17927418e-16]))\n",
|
||||||
|
" fun: 4.861153433422115e-17\n",
|
||||||
|
" message: 'Optimization terminated successfully.'\n",
|
||||||
|
" nfev: 571\n",
|
||||||
|
" nit: 339\n",
|
||||||
|
" status: 0\n",
|
||||||
|
" success: True\n",
|
||||||
|
" x: array([1., 1., 1., 1., 1.])"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
"execution_count": 1,
|
||||||
|
"metadata": {},
|
||||||
|
"output_type": "execute_result"
|
||||||
|
}
|
||||||
|
],
|
||||||
|
"source": [
|
||||||
|
"import numpy as np\n",
|
||||||
|
"from scipy.optimize import minimize\n",
|
||||||
|
"\n",
|
||||||
|
"\n",
|
||||||
|
"def rosen(x):\n",
|
||||||
|
" \"\"\"The Rosenbrock function\"\"\"\n",
|
||||||
|
" return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)\n",
|
||||||
|
"\n",
|
||||||
|
"x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])\n",
|
||||||
|
"minimize(rosen, x0, method='nelder-mead', options={'xtol': 1e-8, 'disp': True})"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "code",
|
||||||
|
"execution_count": 2,
|
||||||
|
"metadata": {},
|
||||||
|
"outputs": [
|
||||||
|
{
|
||||||
|
"name": "stdout",
|
||||||
|
"output_type": "stream",
|
||||||
|
"text": [
|
||||||
|
"Help on function minimize in module scipy.optimize._minimize:\n",
|
||||||
|
"\n",
|
||||||
|
"minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)\n",
|
||||||
|
" Minimization of scalar function of one or more variables.\n",
|
||||||
|
" \n",
|
||||||
|
" Parameters\n",
|
||||||
|
" ----------\n",
|
||||||
|
" fun : callable\n",
|
||||||
|
" The objective function to be minimized.\n",
|
||||||
|
" \n",
|
||||||
|
" ``fun(x, *args) -> float``\n",
|
||||||
|
" \n",
|
||||||
|
" where x is an 1-D array with shape (n,) and `args`\n",
|
||||||
|
" is a tuple of the fixed parameters needed to completely\n",
|
||||||
|
" specify the function.\n",
|
||||||
|
" x0 : ndarray, shape (n,)\n",
|
||||||
|
" Initial guess. Array of real elements of size (n,),\n",
|
||||||
|
" where 'n' is the number of independent variables.\n",
|
||||||
|
" args : tuple, optional\n",
|
||||||
|
" Extra arguments passed to the objective function and its\n",
|
||||||
|
" derivatives (`fun`, `jac` and `hess` functions).\n",
|
||||||
|
" method : str or callable, optional\n",
|
||||||
|
" Type of solver. Should be one of\n",
|
||||||
|
" \n",
|
||||||
|
" - 'Nelder-Mead' :ref:`(see here) <optimize.minimize-neldermead>`\n",
|
||||||
|
" - 'Powell' :ref:`(see here) <optimize.minimize-powell>`\n",
|
||||||
|
" - 'CG' :ref:`(see here) <optimize.minimize-cg>`\n",
|
||||||
|
" - 'BFGS' :ref:`(see here) <optimize.minimize-bfgs>`\n",
|
||||||
|
" - 'Newton-CG' :ref:`(see here) <optimize.minimize-newtoncg>`\n",
|
||||||
|
" - 'L-BFGS-B' :ref:`(see here) <optimize.minimize-lbfgsb>`\n",
|
||||||
|
" - 'TNC' :ref:`(see here) <optimize.minimize-tnc>`\n",
|
||||||
|
" - 'COBYLA' :ref:`(see here) <optimize.minimize-cobyla>`\n",
|
||||||
|
" - 'SLSQP' :ref:`(see here) <optimize.minimize-slsqp>`\n",
|
||||||
|
" - 'trust-constr':ref:`(see here) <optimize.minimize-trustconstr>`\n",
|
||||||
|
" - 'dogleg' :ref:`(see here) <optimize.minimize-dogleg>`\n",
|
||||||
|
" - 'trust-ncg' :ref:`(see here) <optimize.minimize-trustncg>`\n",
|
||||||
|
" - 'trust-exact' :ref:`(see here) <optimize.minimize-trustexact>`\n",
|
||||||
|
" - 'trust-krylov' :ref:`(see here) <optimize.minimize-trustkrylov>`\n",
|
||||||
|
" - custom - a callable object (added in version 0.14.0),\n",
|
||||||
|
" see below for description.\n",
|
||||||
|
" \n",
|
||||||
|
" If not given, chosen to be one of ``BFGS``, ``L-BFGS-B``, ``SLSQP``,\n",
|
||||||
|
" depending if the problem has constraints or bounds.\n",
|
||||||
|
" jac : {callable, '2-point', '3-point', 'cs', bool}, optional\n",
|
||||||
|
" Method for computing the gradient vector. Only for CG, BFGS,\n",
|
||||||
|
" Newton-CG, L-BFGS-B, TNC, SLSQP, dogleg, trust-ncg, trust-krylov,\n",
|
||||||
|
" trust-exact and trust-constr. If it is a callable, it should be a\n",
|
||||||
|
" function that returns the gradient vector:\n",
|
||||||
|
" \n",
|
||||||
|
" ``jac(x, *args) -> array_like, shape (n,)``\n",
|
||||||
|
" \n",
|
||||||
|
" where x is an array with shape (n,) and `args` is a tuple with\n",
|
||||||
|
" the fixed parameters. Alternatively, the keywords\n",
|
||||||
|
" {'2-point', '3-point', 'cs'} select a finite\n",
|
||||||
|
" difference scheme for numerical estimation of the gradient. Options\n",
|
||||||
|
" '3-point' and 'cs' are available only to 'trust-constr'.\n",
|
||||||
|
" If `jac` is a Boolean and is True, `fun` is assumed to return the\n",
|
||||||
|
" gradient along with the objective function. If False, the gradient\n",
|
||||||
|
" will be estimated using '2-point' finite difference estimation.\n",
|
||||||
|
" hess : {callable, '2-point', '3-point', 'cs', HessianUpdateStrategy}, optional\n",
|
||||||
|
" Method for computing the Hessian matrix. Only for Newton-CG, dogleg,\n",
|
||||||
|
" trust-ncg, trust-krylov, trust-exact and trust-constr. If it is\n",
|
||||||
|
" callable, it should return the Hessian matrix:\n",
|
||||||
|
" \n",
|
||||||
|
" ``hess(x, *args) -> {LinearOperator, spmatrix, array}, (n, n)``\n",
|
||||||
|
" \n",
|
||||||
|
" where x is a (n,) ndarray and `args` is a tuple with the fixed\n",
|
||||||
|
" parameters. LinearOperator and sparse matrix returns are\n",
|
||||||
|
" allowed only for 'trust-constr' method. Alternatively, the keywords\n",
|
||||||
|
" {'2-point', '3-point', 'cs'} select a finite difference scheme\n",
|
||||||
|
" for numerical estimation. Or, objects implementing\n",
|
||||||
|
" `HessianUpdateStrategy` interface can be used to approximate\n",
|
||||||
|
" the Hessian. Available quasi-Newton methods implementing\n",
|
||||||
|
" this interface are:\n",
|
||||||
|
" \n",
|
||||||
|
" - `BFGS`;\n",
|
||||||
|
" - `SR1`.\n",
|
||||||
|
" \n",
|
||||||
|
" Whenever the gradient is estimated via finite-differences,\n",
|
||||||
|
" the Hessian cannot be estimated with options\n",
|
||||||
|
" {'2-point', '3-point', 'cs'} and needs to be\n",
|
||||||
|
" estimated using one of the quasi-Newton strategies.\n",
|
||||||
|
" Finite-difference options {'2-point', '3-point', 'cs'} and\n",
|
||||||
|
" `HessianUpdateStrategy` are available only for 'trust-constr' method.\n",
|
||||||
|
" hessp : callable, optional\n",
|
||||||
|
" Hessian of objective function times an arbitrary vector p. Only for\n",
|
||||||
|
" Newton-CG, trust-ncg, trust-krylov, trust-constr.\n",
|
||||||
|
" Only one of `hessp` or `hess` needs to be given. If `hess` is\n",
|
||||||
|
" provided, then `hessp` will be ignored. `hessp` must compute the\n",
|
||||||
|
" Hessian times an arbitrary vector:\n",
|
||||||
|
" \n",
|
||||||
|
" ``hessp(x, p, *args) -> ndarray shape (n,)``\n",
|
||||||
|
" \n",
|
||||||
|
" where x is a (n,) ndarray, p is an arbitrary vector with\n",
|
||||||
|
" dimension (n,) and `args` is a tuple with the fixed\n",
|
||||||
|
" parameters.\n",
|
||||||
|
" bounds : sequence or `Bounds`, optional\n",
|
||||||
|
" Bounds on variables for L-BFGS-B, TNC, SLSQP and\n",
|
||||||
|
" trust-constr methods. There are two ways to specify the bounds:\n",
|
||||||
|
" \n",
|
||||||
|
" 1. Instance of `Bounds` class.\n",
|
||||||
|
" 2. Sequence of ``(min, max)`` pairs for each element in `x`. None\n",
|
||||||
|
" is used to specify no bound.\n",
|
||||||
|
" \n",
|
||||||
|
" constraints : {Constraint, dict} or List of {Constraint, dict}, optional\n",
|
||||||
|
" Constraints definition (only for COBYLA, SLSQP and trust-constr).\n",
|
||||||
|
" Constraints for 'trust-constr' are defined as a single object or a\n",
|
||||||
|
" list of objects specifying constraints to the optimization problem.\n",
|
||||||
|
" Available constraints are:\n",
|
||||||
|
" \n",
|
||||||
|
" - `LinearConstraint`\n",
|
||||||
|
" - `NonlinearConstraint`\n",
|
||||||
|
" \n",
|
||||||
|
" Constraints for COBYLA, SLSQP are defined as a list of dictionaries.\n",
|
||||||
|
" Each dictionary with fields:\n",
|
||||||
|
" \n",
|
||||||
|
" type : str\n",
|
||||||
|
" Constraint type: 'eq' for equality, 'ineq' for inequality.\n",
|
||||||
|
" fun : callable\n",
|
||||||
|
" The function defining the constraint.\n",
|
||||||
|
" jac : callable, optional\n",
|
||||||
|
" The Jacobian of `fun` (only for SLSQP).\n",
|
||||||
|
" args : sequence, optional\n",
|
||||||
|
" Extra arguments to be passed to the function and Jacobian.\n",
|
||||||
|
" \n",
|
||||||
|
" Equality constraint means that the constraint function result is to\n",
|
||||||
|
" be zero whereas inequality means that it is to be non-negative.\n",
|
||||||
|
" Note that COBYLA only supports inequality constraints.\n",
|
||||||
|
" tol : float, optional\n",
|
||||||
|
" Tolerance for termination. For detailed control, use solver-specific\n",
|
||||||
|
" options.\n",
|
||||||
|
" options : dict, optional\n",
|
||||||
|
" A dictionary of solver options. All methods accept the following\n",
|
||||||
|
" generic options:\n",
|
||||||
|
" \n",
|
||||||
|
" maxiter : int\n",
|
||||||
|
" Maximum number of iterations to perform.\n",
|
||||||
|
" disp : bool\n",
|
||||||
|
" Set to True to print convergence messages.\n",
|
||||||
|
" \n",
|
||||||
|
" For method-specific options, see :func:`show_options()`.\n",
|
||||||
|
" callback : callable, optional\n",
|
||||||
|
" Called after each iteration. For 'trust-constr' it is a callable with\n",
|
||||||
|
" the signature:\n",
|
||||||
|
" \n",
|
||||||
|
" ``callback(xk, OptimizeResult state) -> bool``\n",
|
||||||
|
" \n",
|
||||||
|
" where ``xk`` is the current parameter vector. and ``state``\n",
|
||||||
|
" is an `OptimizeResult` object, with the same fields\n",
|
||||||
|
" as the ones from the return. If callback returns True\n",
|
||||||
|
" the algorithm execution is terminated.\n",
|
||||||
|
" For all the other methods, the signature is:\n",
|
||||||
|
" \n",
|
||||||
|
" ``callback(xk)``\n",
|
||||||
|
" \n",
|
||||||
|
" where ``xk`` is the current parameter vector.\n",
|
||||||
|
" \n",
|
||||||
|
" Returns\n",
|
||||||
|
" -------\n",
|
||||||
|
" res : OptimizeResult\n",
|
||||||
|
" The optimization result represented as a ``OptimizeResult`` object.\n",
|
||||||
|
" Important attributes are: ``x`` the solution array, ``success`` a\n",
|
||||||
|
" Boolean flag indicating if the optimizer exited successfully and\n",
|
||||||
|
" ``message`` which describes the cause of the termination. See\n",
|
||||||
|
" `OptimizeResult` for a description of other attributes.\n",
|
||||||
|
" \n",
|
||||||
|
" \n",
|
||||||
|
" See also\n",
|
||||||
|
" --------\n",
|
||||||
|
" minimize_scalar : Interface to minimization algorithms for scalar\n",
|
||||||
|
" univariate functions\n",
|
||||||
|
" show_options : Additional options accepted by the solvers\n",
|
||||||
|
" \n",
|
||||||
|
" Notes\n",
|
||||||
|
" -----\n",
|
||||||
|
" This section describes the available solvers that can be selected by the\n",
|
||||||
|
" 'method' parameter. The default method is *BFGS*.\n",
|
||||||
|
" \n",
|
||||||
|
" **Unconstrained minimization**\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`Nelder-Mead <optimize.minimize-neldermead>` uses the\n",
|
||||||
|
" Simplex algorithm [1]_, [2]_. This algorithm is robust in many\n",
|
||||||
|
" applications. However, if numerical computation of derivative can be\n",
|
||||||
|
" trusted, other algorithms using the first and/or second derivatives\n",
|
||||||
|
" information might be preferred for their better performance in\n",
|
||||||
|
" general.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`Powell <optimize.minimize-powell>` is a modification\n",
|
||||||
|
" of Powell's method [3]_, [4]_ which is a conjugate direction\n",
|
||||||
|
" method. It performs sequential one-dimensional minimizations along\n",
|
||||||
|
" each vector of the directions set (`direc` field in `options` and\n",
|
||||||
|
" `info`), which is updated at each iteration of the main\n",
|
||||||
|
" minimization loop. The function need not be differentiable, and no\n",
|
||||||
|
" derivatives are taken.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`CG <optimize.minimize-cg>` uses a nonlinear conjugate\n",
|
||||||
|
" gradient algorithm by Polak and Ribiere, a variant of the\n",
|
||||||
|
" Fletcher-Reeves method described in [5]_ pp. 120-122. Only the\n",
|
||||||
|
" first derivatives are used.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`BFGS <optimize.minimize-bfgs>` uses the quasi-Newton\n",
|
||||||
|
" method of Broyden, Fletcher, Goldfarb, and Shanno (BFGS) [5]_\n",
|
||||||
|
" pp. 136. It uses the first derivatives only. BFGS has proven good\n",
|
||||||
|
" performance even for non-smooth optimizations. This method also\n",
|
||||||
|
" returns an approximation of the Hessian inverse, stored as\n",
|
||||||
|
" `hess_inv` in the OptimizeResult object.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`Newton-CG <optimize.minimize-newtoncg>` uses a\n",
|
||||||
|
" Newton-CG algorithm [5]_ pp. 168 (also known as the truncated\n",
|
||||||
|
" Newton method). It uses a CG method to the compute the search\n",
|
||||||
|
" direction. See also *TNC* method for a box-constrained\n",
|
||||||
|
" minimization with a similar algorithm. Suitable for large-scale\n",
|
||||||
|
" problems.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`dogleg <optimize.minimize-dogleg>` uses the dog-leg\n",
|
||||||
|
" trust-region algorithm [5]_ for unconstrained minimization. This\n",
|
||||||
|
" algorithm requires the gradient and Hessian; furthermore the\n",
|
||||||
|
" Hessian is required to be positive definite.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`trust-ncg <optimize.minimize-trustncg>` uses the\n",
|
||||||
|
" Newton conjugate gradient trust-region algorithm [5]_ for\n",
|
||||||
|
" unconstrained minimization. This algorithm requires the gradient\n",
|
||||||
|
" and either the Hessian or a function that computes the product of\n",
|
||||||
|
" the Hessian with a given vector. Suitable for large-scale problems.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`trust-krylov <optimize.minimize-trustkrylov>` uses\n",
|
||||||
|
" the Newton GLTR trust-region algorithm [14]_, [15]_ for unconstrained\n",
|
||||||
|
" minimization. This algorithm requires the gradient\n",
|
||||||
|
" and either the Hessian or a function that computes the product of\n",
|
||||||
|
" the Hessian with a given vector. Suitable for large-scale problems.\n",
|
||||||
|
" On indefinite problems it requires usually less iterations than the\n",
|
||||||
|
" `trust-ncg` method and is recommended for medium and large-scale problems.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`trust-exact <optimize.minimize-trustexact>`\n",
|
||||||
|
" is a trust-region method for unconstrained minimization in which\n",
|
||||||
|
" quadratic subproblems are solved almost exactly [13]_. This\n",
|
||||||
|
" algorithm requires the gradient and the Hessian (which is\n",
|
||||||
|
" *not* required to be positive definite). It is, in many\n",
|
||||||
|
" situations, the Newton method to converge in fewer iteraction\n",
|
||||||
|
" and the most recommended for small and medium-size problems.\n",
|
||||||
|
" \n",
|
||||||
|
" **Bound-Constrained minimization**\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`L-BFGS-B <optimize.minimize-lbfgsb>` uses the L-BFGS-B\n",
|
||||||
|
" algorithm [6]_, [7]_ for bound constrained minimization.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`TNC <optimize.minimize-tnc>` uses a truncated Newton\n",
|
||||||
|
" algorithm [5]_, [8]_ to minimize a function with variables subject\n",
|
||||||
|
" to bounds. This algorithm uses gradient information; it is also\n",
|
||||||
|
" called Newton Conjugate-Gradient. It differs from the *Newton-CG*\n",
|
||||||
|
" method described above as it wraps a C implementation and allows\n",
|
||||||
|
" each variable to be given upper and lower bounds.\n",
|
||||||
|
" \n",
|
||||||
|
" **Constrained Minimization**\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`COBYLA <optimize.minimize-cobyla>` uses the\n",
|
||||||
|
" Constrained Optimization BY Linear Approximation (COBYLA) method\n",
|
||||||
|
" [9]_, [10]_, [11]_. The algorithm is based on linear\n",
|
||||||
|
" approximations to the objective function and each constraint. The\n",
|
||||||
|
" method wraps a FORTRAN implementation of the algorithm. The\n",
|
||||||
|
" constraints functions 'fun' may return either a single number\n",
|
||||||
|
" or an array or list of numbers.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`SLSQP <optimize.minimize-slsqp>` uses Sequential\n",
|
||||||
|
" Least SQuares Programming to minimize a function of several\n",
|
||||||
|
" variables with any combination of bounds, equality and inequality\n",
|
||||||
|
" constraints. The method wraps the SLSQP Optimization subroutine\n",
|
||||||
|
" originally implemented by Dieter Kraft [12]_. Note that the\n",
|
||||||
|
" wrapper handles infinite values in bounds by converting them into\n",
|
||||||
|
" large floating values.\n",
|
||||||
|
" \n",
|
||||||
|
" Method :ref:`trust-constr <optimize.minimize-trustconstr>` is a\n",
|
||||||
|
" trust-region algorithm for constrained optimization. It swiches\n",
|
||||||
|
" between two implementations depending on the problem definition.\n",
|
||||||
|
" It is the most versatile constrained minimization algorithm\n",
|
||||||
|
" implemented in SciPy and the most appropriate for large-scale problems.\n",
|
||||||
|
" For equality constrained problems it is an implementation of Byrd-Omojokun\n",
|
||||||
|
" Trust-Region SQP method described in [17]_ and in [5]_, p. 549. When\n",
|
||||||
|
" inequality constraints are imposed as well, it swiches to the trust-region\n",
|
||||||
|
" interior point method described in [16]_. This interior point algorithm,\n",
|
||||||
|
" in turn, solves inequality constraints by introducing slack variables\n",
|
||||||
|
" and solving a sequence of equality-constrained barrier problems\n",
|
||||||
|
" for progressively smaller values of the barrier parameter.\n",
|
||||||
|
" The previously described equality constrained SQP method is\n",
|
||||||
|
" used to solve the subproblems with increasing levels of accuracy\n",
|
||||||
|
" as the iterate gets closer to a solution.\n",
|
||||||
|
" \n",
|
||||||
|
" **Finite-Difference Options**\n",
|
||||||
|
" \n",
|
||||||
|
" For Method :ref:`trust-constr <optimize.minimize-trustconstr>`\n",
|
||||||
|
" the gradient and the Hessian may be approximated using\n",
|
||||||
|
" three finite-difference schemes: {'2-point', '3-point', 'cs'}.\n",
|
||||||
|
" The scheme 'cs' is, potentially, the most accurate but it\n",
|
||||||
|
" requires the function to correctly handles complex inputs and to\n",
|
||||||
|
" be differentiable in the complex plane. The scheme '3-point' is more\n",
|
||||||
|
" accurate than '2-point' but requires twice as much operations.\n",
|
||||||
|
" \n",
|
||||||
|
" **Custom minimizers**\n",
|
||||||
|
" \n",
|
||||||
|
" It may be useful to pass a custom minimization method, for example\n",
|
||||||
|
" when using a frontend to this method such as `scipy.optimize.basinhopping`\n",
|
||||||
|
" or a different library. You can simply pass a callable as the ``method``\n",
|
||||||
|
" parameter.\n",
|
||||||
|
" \n",
|
||||||
|
" The callable is called as ``method(fun, x0, args, **kwargs, **options)``\n",
|
||||||
|
" where ``kwargs`` corresponds to any other parameters passed to `minimize`\n",
|
||||||
|
" (such as `callback`, `hess`, etc.), except the `options` dict, which has\n",
|
||||||
|
" its contents also passed as `method` parameters pair by pair. Also, if\n",
|
||||||
|
" `jac` has been passed as a bool type, `jac` and `fun` are mangled so that\n",
|
||||||
|
" `fun` returns just the function values and `jac` is converted to a function\n",
|
||||||
|
" returning the Jacobian. The method shall return an ``OptimizeResult``\n",
|
||||||
|
" object.\n",
|
||||||
|
" \n",
|
||||||
|
" The provided `method` callable must be able to accept (and possibly ignore)\n",
|
||||||
|
" arbitrary parameters; the set of parameters accepted by `minimize` may\n",
|
||||||
|
" expand in future versions and then these parameters will be passed to\n",
|
||||||
|
" the method. You can find an example in the scipy.optimize tutorial.\n",
|
||||||
|
" \n",
|
||||||
|
" .. versionadded:: 0.11.0\n",
|
||||||
|
" \n",
|
||||||
|
" References\n",
|
||||||
|
" ----------\n",
|
||||||
|
" .. [1] Nelder, J A, and R Mead. 1965. A Simplex Method for Function\n",
|
||||||
|
" Minimization. The Computer Journal 7: 308-13.\n",
|
||||||
|
" .. [2] Wright M H. 1996. Direct search methods: Once scorned, now\n",
|
||||||
|
" respectable, in Numerical Analysis 1995: Proceedings of the 1995\n",
|
||||||
|
" Dundee Biennial Conference in Numerical Analysis (Eds. D F\n",
|
||||||
|
" Griffiths and G A Watson). Addison Wesley Longman, Harlow, UK.\n",
|
||||||
|
" 191-208.\n",
|
||||||
|
" .. [3] Powell, M J D. 1964. An efficient method for finding the minimum of\n",
|
||||||
|
" a function of several variables without calculating derivatives. The\n",
|
||||||
|
" Computer Journal 7: 155-162.\n",
|
||||||
|
" .. [4] Press W, S A Teukolsky, W T Vetterling and B P Flannery.\n",
|
||||||
|
" Numerical Recipes (any edition), Cambridge University Press.\n",
|
||||||
|
" .. [5] Nocedal, J, and S J Wright. 2006. Numerical Optimization.\n",
|
||||||
|
" Springer New York.\n",
|
||||||
|
" .. [6] Byrd, R H and P Lu and J. Nocedal. 1995. A Limited Memory\n",
|
||||||
|
" Algorithm for Bound Constrained Optimization. SIAM Journal on\n",
|
||||||
|
" Scientific and Statistical Computing 16 (5): 1190-1208.\n",
|
||||||
|
" .. [7] Zhu, C and R H Byrd and J Nocedal. 1997. L-BFGS-B: Algorithm\n",
|
||||||
|
" 778: L-BFGS-B, FORTRAN routines for large scale bound constrained\n",
|
||||||
|
" optimization. ACM Transactions on Mathematical Software 23 (4):\n",
|
||||||
|
" 550-560.\n",
|
||||||
|
" .. [8] Nash, S G. Newton-Type Minimization Via the Lanczos Method.\n",
|
||||||
|
" 1984. SIAM Journal of Numerical Analysis 21: 770-778.\n",
|
||||||
|
" .. [9] Powell, M J D. A direct search optimization method that models\n",
|
||||||
|
" the objective and constraint functions by linear interpolation.\n",
|
||||||
|
" 1994. Advances in Optimization and Numerical Analysis, eds. S. Gomez\n",
|
||||||
|
" and J-P Hennart, Kluwer Academic (Dordrecht), 51-67.\n",
|
||||||
|
" .. [10] Powell M J D. Direct search algorithms for optimization\n",
|
||||||
|
" calculations. 1998. Acta Numerica 7: 287-336.\n",
|
||||||
|
" .. [11] Powell M J D. A view of algorithms for optimization without\n",
|
||||||
|
" derivatives. 2007.Cambridge University Technical Report DAMTP\n",
|
||||||
|
" 2007/NA03\n",
|
||||||
|
" .. [12] Kraft, D. A software package for sequential quadratic\n",
|
||||||
|
" programming. 1988. Tech. Rep. DFVLR-FB 88-28, DLR German Aerospace\n",
|
||||||
|
" Center -- Institute for Flight Mechanics, Koln, Germany.\n",
|
||||||
|
" .. [13] Conn, A. R., Gould, N. I., and Toint, P. L.\n",
|
||||||
|
" Trust region methods. 2000. Siam. pp. 169-200.\n",
|
||||||
|
" .. [14] F. Lenders, C. Kirches, A. Potschka: \"trlib: A vector-free\n",
|
||||||
|
" implementation of the GLTR method for iterative solution of\n",
|
||||||
|
" the trust region problem\", https://arxiv.org/abs/1611.04718\n",
|
||||||
|
" .. [15] N. Gould, S. Lucidi, M. Roma, P. Toint: \"Solving the\n",
|
||||||
|
" Trust-Region Subproblem using the Lanczos Method\",\n",
|
||||||
|
" SIAM J. Optim., 9(2), 504--525, (1999).\n",
|
||||||
|
" .. [16] Byrd, Richard H., Mary E. Hribar, and Jorge Nocedal. 1999.\n",
|
||||||
|
" An interior point algorithm for large-scale nonlinear programming.\n",
|
||||||
|
" SIAM Journal on Optimization 9.4: 877-900.\n",
|
||||||
|
" .. [17] Lalee, Marucha, Jorge Nocedal, and Todd Plantega. 1998. On the\n",
|
||||||
|
" implementation of an algorithm for large-scale equality constrained\n",
|
||||||
|
" optimization. SIAM Journal on Optimization 8.3: 682-706.\n",
|
||||||
|
" \n",
|
||||||
|
" Examples\n",
|
||||||
|
" --------\n",
|
||||||
|
" Let us consider the problem of minimizing the Rosenbrock function. This\n",
|
||||||
|
" function (and its respective derivatives) is implemented in `rosen`\n",
|
||||||
|
" (resp. `rosen_der`, `rosen_hess`) in the `scipy.optimize`.\n",
|
||||||
|
" \n",
|
||||||
|
" >>> from scipy.optimize import minimize, rosen, rosen_der\n",
|
||||||
|
" \n",
|
||||||
|
" A simple application of the *Nelder-Mead* method is:\n",
|
||||||
|
" \n",
|
||||||
|
" >>> x0 = [1.3, 0.7, 0.8, 1.9, 1.2]\n",
|
||||||
|
" >>> res = minimize(rosen, x0, method='Nelder-Mead', tol=1e-6)\n",
|
||||||
|
" >>> res.x\n",
|
||||||
|
" array([ 1., 1., 1., 1., 1.])\n",
|
||||||
|
" \n",
|
||||||
|
" Now using the *BFGS* algorithm, using the first derivative and a few\n",
|
||||||
|
" options:\n",
|
||||||
|
" \n",
|
||||||
|
" >>> res = minimize(rosen, x0, method='BFGS', jac=rosen_der,\n",
|
||||||
|
" ... options={'gtol': 1e-6, 'disp': True})\n",
|
||||||
|
" Optimization terminated successfully.\n",
|
||||||
|
" Current function value: 0.000000\n",
|
||||||
|
" Iterations: 26\n",
|
||||||
|
" Function evaluations: 31\n",
|
||||||
|
" Gradient evaluations: 31\n",
|
||||||
|
" >>> res.x\n",
|
||||||
|
" array([ 1., 1., 1., 1., 1.])\n",
|
||||||
|
" >>> print(res.message)\n",
|
||||||
|
" Optimization terminated successfully.\n",
|
||||||
|
" >>> res.hess_inv\n",
|
||||||
|
" array([[ 0.00749589, 0.01255155, 0.02396251, 0.04750988, 0.09495377], # may vary\n",
|
||||||
|
" [ 0.01255155, 0.02510441, 0.04794055, 0.09502834, 0.18996269],\n",
|
||||||
|
" [ 0.02396251, 0.04794055, 0.09631614, 0.19092151, 0.38165151],\n",
|
||||||
|
" [ 0.04750988, 0.09502834, 0.19092151, 0.38341252, 0.7664427 ],\n",
|
||||||
|
" [ 0.09495377, 0.18996269, 0.38165151, 0.7664427, 1.53713523]])\n",
|
||||||
|
" \n",
|
||||||
|
" \n",
|
||||||
|
" Next, consider a minimization problem with several constraints (namely\n",
|
||||||
|
" Example 16.4 from [5]_). The objective function is:\n",
|
||||||
|
" \n",
|
||||||
|
" >>> fun = lambda x: (x[0] - 1)**2 + (x[1] - 2.5)**2\n",
|
||||||
|
" \n",
|
||||||
|
" There are three constraints defined as:\n",
|
||||||
|
" \n",
|
||||||
|
" >>> cons = ({'type': 'ineq', 'fun': lambda x: x[0] - 2 * x[1] + 2},\n",
|
||||||
|
" ... {'type': 'ineq', 'fun': lambda x: -x[0] - 2 * x[1] + 6},\n",
|
||||||
|
" ... {'type': 'ineq', 'fun': lambda x: -x[0] + 2 * x[1] + 2})\n",
|
||||||
|
" \n",
|
||||||
|
" And variables must be positive, hence the following bounds:\n",
|
||||||
|
" \n",
|
||||||
|
" >>> bnds = ((0, None), (0, None))\n",
|
||||||
|
" \n",
|
||||||
|
" The optimization problem is solved using the SLSQP method as:\n",
|
||||||
|
" \n",
|
||||||
|
" >>> res = minimize(fun, (2, 0), method='SLSQP', bounds=bnds,\n",
|
||||||
|
" ... constraints=cons)\n",
|
||||||
|
" \n",
|
||||||
|
" It should converge to the theoretical solution (1.4 ,1.7).\n",
|
||||||
|
"\n"
|
||||||
|
]
|
||||||
|
}
|
||||||
|
],
|
||||||
|
"source": [
|
||||||
|
"help(minimize)"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "slide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"## Первые производные"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"### Наискорейший подъем (спуск)\n",
|
||||||
|
"Направление на максимум всегда в направлении градиента функции:\n",
|
||||||
|
"\n",
|
||||||
|
"$$ \\theta_{k+1} = \\theta_k + \\beta_k \\nabla L $$\n",
|
||||||
|
"\n",
|
||||||
|
"* Не понятно, как определять $\\beta$\n",
|
||||||
|
"* Не понятно, когда останавливаться."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "fragment"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"Модификация метода - метод сопряженных градиентов на самом деле требует второй производной."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "slide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"## Вторые производные"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"Главная формула:\n",
|
||||||
|
"\n",
|
||||||
|
"$$ L(\\theta) = L(\\theta_0) + \\nabla L( \\theta - \\theta_0) + \\frac{1}{2} (\\theta-\\theta_0)^T H (\\theta-\\theta_0) + o(\\theta-\\theta_0)$$"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"### Метод Ньютона\n",
|
||||||
|
"\n",
|
||||||
|
"$$\\nabla f(\\theta_k) + H(\\theta_k)(\\theta_{k+1} - \\theta_k) = 0$$\n",
|
||||||
|
"\n",
|
||||||
|
"$$ \\theta_{k+1} = \\theta_k - H^{-1}(\\theta_k)\\nabla L(\\theta_k) $$"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "fragment"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"Можно добавить выбор шага:\n",
|
||||||
|
"\n",
|
||||||
|
"$$ \\theta_{k+1} = \\theta_k - \\lambda_i H^{-1}(\\theta_k)\\nabla L(\\theta_k) $$"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "code",
|
||||||
|
"execution_count": 12,
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "fragment"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"outputs": [
|
||||||
|
{
|
||||||
|
"data": {
|
||||||
|
"text/plain": [
|
||||||
|
"1.0000000000000016"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
"execution_count": 12,
|
||||||
|
"metadata": {},
|
||||||
|
"output_type": "execute_result"
|
||||||
|
}
|
||||||
|
],
|
||||||
|
"source": [
|
||||||
|
"from scipy import optimize\n",
|
||||||
|
"optimize.newton(lambda x: x**3 - 1, 1.5)"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"### Методы с переменной метрикой\n",
|
||||||
|
"\n",
|
||||||
|
"* Вычислять $\\nabla L$ и $H$ очень дорого\n",
|
||||||
|
"* Давайте вычислять их итеративно.\n",
|
||||||
|
"\n",
|
||||||
|
"Примеры: \n",
|
||||||
|
"* MINUIT\n",
|
||||||
|
"* scipy `minimize(method=’L-BFGS-B’)`"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "slide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"# Случай наименьших квадратов"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"В случае анализа спектров имеем:\n",
|
||||||
|
"\n",
|
||||||
|
"$$ L(X | \\theta) = \\prod p_i (x_i | \\theta)$$\n",
|
||||||
|
"\n",
|
||||||
|
"Или:\n",
|
||||||
|
"\n",
|
||||||
|
"$$\\ln{ L(X | \\theta)} = \\sum \\ln{ p_i (x_i | \\theta)}$$\n",
|
||||||
|
"\n",
|
||||||
|
"В случае нормальных распределений:\n",
|
||||||
|
"\n",
|
||||||
|
"$$\\ln{ L(X | \\theta)} \\sim \\sum{ \\left( \\frac{y_i - \\mu(x_i, \\theta)}{\\sigma_i} \\right)^2 }$$"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"### Метод Гаусса-Ньютона\n",
|
||||||
|
"Пусть:\n",
|
||||||
|
"$$r_i = \\frac{y_i - \\mu(x_i, \\theta)}{\\sigma_i}$$ \n",
|
||||||
|
"$$J_{ij} = \\frac{\\partial r_i}{\\partial \\theta_j} = - \\frac{\\partial \\mu(x_i, \\theta)}{\\sigma_i \\partial \\theta_j}$$\n",
|
||||||
|
"\n",
|
||||||
|
"Тогда:\n",
|
||||||
|
"\n",
|
||||||
|
"$$ \\theta_{(k+1)} = \\theta_{(k)} - \\left( J^TJ \\right)^{-1}J^Tr(\\theta)$$"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"### Алгоритм Левенберга — Марквардта\n",
|
||||||
|
"\n",
|
||||||
|
"$$ \\theta_{(k+1)} = \\theta_{(k)} + \\delta$$\n",
|
||||||
|
"\n",
|
||||||
|
"$$ (J^TJ + \\lambda I)\\delta = J^Tr(\\theta)$$\n",
|
||||||
|
"\n",
|
||||||
|
"При этом $\\lambda$ - фактор регуляризации, выбирается произвольным образом."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {
|
||||||
|
"slideshow": {
|
||||||
|
"slide_type": "subslide"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"source": [
|
||||||
|
"### Метод квазиоптимальных весов\n",
|
||||||
|
"Идея:\n",
|
||||||
|
" Есть некоторая статистика (функция данных) $f(x)$. Для оптимального решения среднее от этой функции по экспериментальным данным и по модели должны совпадать:\n",
|
||||||
|
"$$ E_\\theta(f(x)) = \\sum_i{f(x_i)} $$\n",
|
||||||
|
"\n",
|
||||||
|
"Можно показать, что оптимальная эффективность получается когда\n",
|
||||||
|
"\n",
|
||||||
|
"$$ f = \\frac{\\partial \\ln L}{\\partial \\theta} $$\n",
|
||||||
|
"\n",
|
||||||
|
"В этом случае и если ошибки распределены по Гауссу или Пуассону, решение для оптмального $\\theta$ можно получить как:\n",
|
||||||
|
"\n",
|
||||||
|
"$$ \n",
|
||||||
|
"\\sum_{i}{\\frac{\\mu_{i}\\left( \\mathbf{\\theta},E_{i} \\right) - x_{i}}{\\sigma_{i}^{2}}\\left. \\ \\frac{\\partial\\mu_{i}\\left( \\mathbf{\\theta},E_{i} \\right)}{\\partial\\mathbf{\\theta}} \\right|_{\\mathbf{\\theta}_{\\mathbf{0}}}} = 0. \n",
|
||||||
|
"$$"
|
||||||
|
]
|
||||||
|
}
|
||||||
|
],
|
||||||
|
"metadata": {
|
||||||
|
"celltoolbar": "Slideshow",
|
||||||
|
"hide_input": false,
|
||||||
|
"kernelspec": {
|
||||||
|
"display_name": "Python 3",
|
||||||
|
"language": "python",
|
||||||
|
"name": "python3"
|
||||||
|
},
|
||||||
|
"language_info": {
|
||||||
|
"codemirror_mode": {
|
||||||
|
"name": "ipython",
|
||||||
|
"version": 3
|
||||||
|
},
|
||||||
|
"file_extension": ".py",
|
||||||
|
"mimetype": "text/x-python",
|
||||||
|
"name": "python",
|
||||||
|
"nbconvert_exporter": "python",
|
||||||
|
"pygments_lexer": "ipython3",
|
||||||
|
"version": "3.7.4"
|
||||||
|
},
|
||||||
|
"toc": {
|
||||||
|
"base_numbering": 1,
|
||||||
|
"nav_menu": {},
|
||||||
|
"number_sections": false,
|
||||||
|
"sideBar": false,
|
||||||
|
"skip_h1_title": false,
|
||||||
|
"title_cell": "Table of Contents",
|
||||||
|
"title_sidebar": "Contents",
|
||||||
|
"toc_cell": false,
|
||||||
|
"toc_position": {},
|
||||||
|
"toc_section_display": false,
|
||||||
|
"toc_window_display": false
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"nbformat": 4,
|
||||||
|
"nbformat_minor": 4
|
||||||
|
}
|
||||||
136
notebooks/python/hypotesis.ipynb
Normal file
136
notebooks/python/hypotesis.ipynb
Normal file
@ -0,0 +1,136 @@
|
|||||||
|
{
|
||||||
|
"cells": [
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {},
|
||||||
|
"source": [
|
||||||
|
"# Проверка статистических гипотез\n",
|
||||||
|
"\n",
|
||||||
|
"Задача: есть некоторое статистическое утверждение (гипотеза) $H$ и есть набор экспериментальных данных $X$. Требуется сделать утверждение о степени достоверности гипотезы **H** при заданном наборе $X$.\n",
|
||||||
|
"\n",
|
||||||
|
"В большинстве случаев речь идет о проверке единственной гипотезы, которую принято называть нулевой $H_0$. В отдельных случаях стоит также задача выбора наиболее подходящей гипотезы из набора $H_0,~H_1,~H_2,~...$\n",
|
||||||
|
"\n",
|
||||||
|
"Для формализации процесса проверки гипотезы требуется ввести ФПВ: $f(X|H_0)$, характеризующее вероятность получить заданные наблюдаемые результаты в случае, если гипотеза верна.\n",
|
||||||
|
"\n",
|
||||||
|
"**Замечание** Вообще говоря, уже этого распределеня достаточно для того, чтобы понять, верна гипотеза или нет. Если вероятность получить набор данных велика, то гипотеза наверное не верна. С другой стороны, возникает проблема с тем, что сложно понять, на сколько именно (с какой достоверностью) верна или не верна гипотеза нормировки распределений часто вычисляются не верно.\n",
|
||||||
|
"\n",
|
||||||
|
"Для упрощения процесс принятия решения, используют функцию, называемую проверочной статистикой: $T(X)$, где T - число. Для такой статистики довольно легко построит ФПВ: $g(T|H_0)$."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {},
|
||||||
|
"source": [
|
||||||
|
""
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {},
|
||||||
|
"source": [
|
||||||
|
"Для критерия $T$ вводится понятие критического значения или критической области $T_0$. В случае, если значение $T$ превышает критическое значение (или выходит из критической области), то гипотеза считается не верной. Если значение в области, гипотеза считается верной.\n",
|
||||||
|
"\n",
|
||||||
|
"Величина\n",
|
||||||
|
"$$\n",
|
||||||
|
" \\alpha = \\int_{T_0}^\\inf {g(T|H_0)}\n",
|
||||||
|
"$$\n",
|
||||||
|
"показывает вероятность **ошибки I рода**. То есть вероятность отвергнуть гипотезу, когда она верна. Величину $1-\\alpha$ называют уровнем достоверности критерия.\n",
|
||||||
|
"\n",
|
||||||
|
"В случае, если существует единственная альтернативная (исключающая $H_0$) гипотеза $H_1$, то также можно определить величину **ошибки II рода**, то есть вероятность принять $H_0$ в случае если она не верна:\n",
|
||||||
|
"$$\n",
|
||||||
|
" \\beta = \\int_{-\\inf}^{T_0} {g(T|H_1)}\n",
|
||||||
|
"$$\n",
|
||||||
|
"\n",
|
||||||
|
"Величину $1-\\beta$ называют мощностью критерия при заданной достоверности $1-\\alpha$.\n",
|
||||||
|
"\n",
|
||||||
|
"Среди двух критериев предпочтительным является тот, для которого мощность при той же значимости выше. Критерий, который будет более мощным для всех возможных состояний природы, называют равномерно более мощным критерием."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {},
|
||||||
|
"source": [
|
||||||
|
"## Построение критической области критерия\n"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {},
|
||||||
|
"source": [
|
||||||
|
"Визуально подбро критической области критерия можно сделать следующим образом: \n",
|
||||||
|
"\n",
|
||||||
|
"* Берем распределение $g(T|H_0)$.\n",
|
||||||
|
"* Интегрируем его и получаем интегральное распределение: $G(T|H_0) = \\int{g(T|H_0)}$. При необходимости перенормируем в диапазон [0,1].\n",
|
||||||
|
"* Проводим линию на уровне нужного уровня значимости (например C. L. 95%).\n",
|
||||||
|
"* Пересечение этой линии с графиком проектируется на ось T и это значение и будет означать критическую область."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {},
|
||||||
|
"source": [
|
||||||
|
"## Качество фита (стандартные критерии)\n",
|
||||||
|
"\n",
|
||||||
|
"### Критерий Пирсона\n",
|
||||||
|
"Проверочная статистика:\n",
|
||||||
|
"$$\n",
|
||||||
|
"\\chi^2 = \\sum{\\frac{ (O_i-E_i)^2}{E_i}}\n",
|
||||||
|
"$$\n",
|
||||||
|
"\n",
|
||||||
|
"Асимпототически приближается к $\\chi^2$ распределению.\n",
|
||||||
|
"\n",
|
||||||
|
"\n",
|
||||||
|
"\n",
|
||||||
|
"### Критерий соотношения правдоподобия\n",
|
||||||
|
"\n",
|
||||||
|
"Пусть $\\Theta$ - пространство параметров $\\theta$, а $\\Omega*$ - область пространства парамеров, на принадлежность которой мы хотим проверить данные. В качестве проверочной статиситки выбирается:\n",
|
||||||
|
"$$\n",
|
||||||
|
"\\lambda = \\frac{L(X|\\theta \\in \\Omega)}{L(X|\\theta \\in \\Theta)}\n",
|
||||||
|
"$$\n",
|
||||||
|
"\n",
|
||||||
|
"Величина $-2ln\\lambda$ распределена как $\\chi^2(r)$, где r - количество фиксированных параметров в $\\Omega$"
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "markdown",
|
||||||
|
"metadata": {},
|
||||||
|
"source": [
|
||||||
|
"## Сложные гипотезы\n",
|
||||||
|
"Положим что есть семейство гипотез $H_i$, среди которых надо выбрать наиболее достоверную. Выбор можно сделать двумя способами:\n",
|
||||||
|
"\n",
|
||||||
|
"* Выбираем ту гипотезу, для которой $g(T|H_i)$ максимален.\n",
|
||||||
|
"* Выбираем ту гипотезу, для которой $\\int_T^\\inf{g(T|H_i)}$ максимален.\n",
|
||||||
|
"\n",
|
||||||
|
"Если принять $T = L(X|\\theta)$, то решение по первому методу сводится к методу максимуму правдоподобия."
|
||||||
|
]
|
||||||
|
},
|
||||||
|
{
|
||||||
|
"cell_type": "code",
|
||||||
|
"execution_count": null,
|
||||||
|
"metadata": {},
|
||||||
|
"outputs": [],
|
||||||
|
"source": []
|
||||||
|
}
|
||||||
|
],
|
||||||
|
"metadata": {
|
||||||
|
"kernelspec": {
|
||||||
|
"display_name": "Python 3",
|
||||||
|
"language": "python",
|
||||||
|
"name": "python3"
|
||||||
|
},
|
||||||
|
"language_info": {
|
||||||
|
"codemirror_mode": {
|
||||||
|
"name": "ipython",
|
||||||
|
"version": 3
|
||||||
|
},
|
||||||
|
"file_extension": ".py",
|
||||||
|
"mimetype": "text/x-python",
|
||||||
|
"name": "python",
|
||||||
|
"nbconvert_exporter": "python",
|
||||||
|
"pygments_lexer": "ipython3",
|
||||||
|
"version": "3.7.4"
|
||||||
|
}
|
||||||
|
},
|
||||||
|
"nbformat": 4,
|
||||||
|
"nbformat_minor": 4
|
||||||
|
}
|
||||||
268
notebooks/python/images/Chi-square_cdf.svg
Normal file
268
notebooks/python/images/Chi-square_cdf.svg
Normal file
@ -0,0 +1,268 @@
|
|||||||
|
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
|
||||||
|
<svg id="chi-square_cdf" version="1.1" baseProfile="full" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:ev="http://www.w3.org/2001/xml-events" width="600" height="400">
|
||||||
|
|
||||||
|
<title>Cumulative chi-Square distribution</title>
|
||||||
|
<desc>
|
||||||
|
chi-square distribution
|
||||||
|
F_k(x) = \int_0^x t^(n/2-1) * exp(-t/2) / (2^(n/2) * gamma(n/2)) dt
|
||||||
|
|
||||||
|
from Wikimedia Commons
|
||||||
|
plot-range: 0 to 8
|
||||||
|
plotted with cubic bezier-curves
|
||||||
|
the bezier-controll-points are calculated to give a very accurate result.
|
||||||
|
accuracy is 0.00001 units
|
||||||
|
symbols in "Computer Modern" (TeX) font embedded
|
||||||
|
created with a plain text editor using GNU/Linux
|
||||||
|
|
||||||
|
about: http://commons.wikimedia.org/wiki/Image:chi-square_cdf.svg
|
||||||
|
source: http://commons.wikimedia.org/
|
||||||
|
rights: GNU Free Documentation license,
|
||||||
|
Creative Commons Attribution ShareAlike license
|
||||||
|
</desc>
|
||||||
|
|
||||||
|
<defs>
|
||||||
|
<!-- pstricks-style arrow, zoom 1.5 -->
|
||||||
|
<marker id="Arrow" refX="2.52" refY="2.25" markerUnits="strokeWidth" markerWidth="6" markerHeight="4.5" orient="auto">
|
||||||
|
<path d="M 2.52 2.25 L 0 4.5 L 6 2.25 L 0 0 z"/>
|
||||||
|
</marker>
|
||||||
|
|
||||||
|
<!-- now the used chars in "Computer Modern" font. They are implemented
|
||||||
|
as plain paths and not as glyphs just because it didn't work -->
|
||||||
|
|
||||||
|
<!-- F: horiz-adv-x="643.1"-->
|
||||||
|
<path id="F" d="M 38 0 m 265 325 h 97 c 75 0 83 -16 83 -45 c 0 -7 0 -19 -7 -49 c -2 -5 -3 -9 -3 -11 c 0 -8 6 -12 12 -12 c 10 0 10 3 15 21 l 55 217 c 3 11 3 13 3 16 c 0 2 -2 11 -12 11 c -10 0 -11 -5 -15 -21 c -21 -78 -44 -96 -129 -96 h -91 l 64 254 c 9 35 10 39 54 39 h 132 c 123 0 146 -33 146 -110 c 0 -23 0 -27 -3 -54 c -2 -13 -2 -15 -2 -18 c 0 -5 3 -12 12 -12 c 11 0 12 6 14 25 l 20 173 c 3 27 -2 27 -27 27 h -490 c -20 0 -30 0 -30 -20 c 0 -11 9 -11 28 -11 c 37 0 65 0 65 -18 c 0 -4 0 -6 -5 -24 l -132 -529 c -10 -39 -12 -47 -91 -47 c -17 0 -28 0 -28 -19 c 0 -12 12 -12 15 -12 c 29 0 103 3 132 3 c 33 0 116 -3 149 -3 c 9 0 21 0 21 19 c 0 8 -6 10 -6 11 c -3 1 -5 1 -28 1 c -22 0 -27 0 -52 2 c -29 3 -32 7 -32 20 c 0 2 0 8 4 23 z"/>
|
||||||
|
<!-- k: horiz-adv-x="520.6"-->
|
||||||
|
<path id="k" d="M 55 0 m 232 683 c 0 1 0 11 -13 11 c -23 0 -96 -8 -122 -10 c -8 -1 -19 -2 -19 -20 c 0 -12 9 -12 24 -12 c 48 0 50 -7 50 -17 l -3 -20 l -145 -576 c -4 -14 -4 -16 -4 -22 c 0 -23 20 -28 29 -28 c 13 0 28 9 34 21 c 5 9 50 194 56 219 c 34 -3 116 -19 116 -85 c 0 -7 0 -11 -3 -21 c -2 -12 -4 -24 -4 -35 c 0 -59 40 -99 92 -99 c 30 0 57 16 79 53 c 25 44 36 99 36 101 c 0 10 -9 10 -12 10 c -10 0 -11 -4 -14 -18 c -20 -73 -43 -124 -87 -124 c -19 0 -32 11 -32 47 c 0 17 4 40 8 56 c 4 17 4 21 4 31 c 0 65 -63 94 -148 105 c 31 18 63 50 86 74 c 48 53 94 96 143 96 c 6 0 7 0 9 -1 c 12 -2 13 -2 21 -8 c 2 -1 2 -2 4 -4 c -48 -3 -57 -42 -57 -54 c 0 -16 11 -35 38 -35 c 26 0 55 22 55 61 c 0 30 -23 63 -68 63 c -28 0 -74 -8 -146 -88 c -34 -38 -73 -78 -111 -93 z"/>
|
||||||
|
<!-- x: horiz-adv-x="527.8"-->
|
||||||
|
<path id="x" d="M 29 0 m 305 302 c 6 26 29 118 99 118 c 5 0 29 0 50 -13 c -28 -5 -48 -30 -48 -54 c 0 -16 11 -35 38 -35 c 22 0 54 18 54 58 c 0 52 -59 66 -93 66 c -58 0 -93 -53 -105 -76 c -25 66 -79 76 -108 76 c -104 0 -161 -129 -161 -154 c 0 -10 10 -10 12 -10 c 8 0 11 2 13 11 c 34 106 100 131 134 131 c 19 0 54 -9 54 -67 c 0 -31 -17 -98 -54 -238 c -16 -62 -51 -104 -95 -104 c -6 0 -29 0 -50 13 c 25 5 47 26 47 54 c 0 27 -22 35 -37 35 c -30 0 -55 -26 -55 -58 c 0 -46 50 -66 94 -66 c 66 0 102 70 105 76 c 12 -37 48 -76 108 -76 c 103 0 160 129 160 154 c 0 10 -9 10 -12 10 c -9 0 -11 -4 -13 -11 c -33 -107 -101 -131 -133 -131 c -39 0 -55 32 -55 66 c 0 22 6 44 17 88 z"/>
|
||||||
|
<!-- chi: horiz-adv-x="625.7"-->
|
||||||
|
<path id="chi" d="M 31 0 m 552 403 c 11 11 11 13 11 16 c 0 6 -4 12 -12 12 c -6 0 -10 -5 -16 -12 l -229 -255 c -40 127 -48 152 -71 205 c -11 23 -33 73 -121 73 c -58 0 -84 -52 -84 -66 c 0 -1 0 -10 12 -10 c 9 0 11 6 13 11 c 15 39 47 43 53 43 c 30 0 60 -76 77 -120 c 32 -79 64 -195 64 -198 c 0 -1 0 -3 -8 -11 l -230 -257 c -11 -11 -11 -13 -11 -16 c 0 -6 6 -12 12 -12 c 7 0 12 7 16 11 l 229 257 c 32 -104 44 -143 68 -199 c 13 -30 35 -80 124 -80 c 58 0 85 52 85 65 c 0 5 -2 11 -12 11 c -10 0 -11 -4 -14 -14 c -9 -24 -34 -40 -53 -40 c -51 0 -119 242 -141 319 z"/>
|
||||||
|
<!-- (: horiz-adv-x="388.9"-->
|
||||||
|
<path id="parleft" d="M 99 0 m 232 -240 c 0 3 0 5 -17 22 c -125 126 -157 315 -157 468 c 0 174 38 348 161 473 c 13 12 13 14 13 17 c 0 7 -4 10 -10 10 c -10 0 -100 -68 -159 -195 c -51 -110 -63 -221 -63 -305 c 0 -78 11 -199 66 -312 c 60 -123 146 -188 156 -188 c 6 0 10 3 10 10 z"/>
|
||||||
|
<!-- ): horiz-adv-x="388.9"-->
|
||||||
|
<path id="parright" d="M 57 0 m 232 250 c 0 78 -11 199 -66 312 c -60 123 -146 188 -156 188 c -6 0 -10 -4 -10 -10 c 0 -3 0 -5 19 -23 c 98 -99 155 -258 155 -467 c 0 -171 -37 -347 -161 -473 c -13 -12 -13 -14 -13 -17 c 0 -6 4 -10 10 -10 c 10 0 100 68 159 195 c 51 110 63 221 63 305 z"/>
|
||||||
|
<!-- =: horiz-adv-x="777.8"-->
|
||||||
|
<path id="equal" d="M 56 0 m 631 327 c 15 0 34 0 34 20 c 0 20 -19 20 -33 20 h -599 c -14 0 -33 0 -33 -20 c 0 -20 19 -20 34 -20 z M 90 327 m 598 -194 c 14 0 33 0 33 20 c 0 20 -19 20 -34 20 h -597 c -15 0 -34 0 -34 -20 c 0 -20 19 -20 33 -20 z"/>
|
||||||
|
<!-- 0: horiz-adv-x="500"-->
|
||||||
|
<path id="zero" d="M 39 0 m 421 320 c 0 80 -5 160 -40 234 c -46 96 -128 112 -170 112 c -60 0 -133 -26 -174 -119 c -32 -69 -37 -147 -37 -227 c 0 -75 4 -165 45 -241 c 43 -81 116 -101 165 -101 c 54 0 130 21 174 116 c 32 69 37 147 37 226 z M 460 320 m -211 -320 c -39 0 -98 25 -116 121 c -11 60 -11 152 -11 211 c 0 64 0 130 8 184 c 19 119 94 128 119 128 c 33 0 99 -18 118 -117 c 10 -56 10 -132 10 -195 c 0 -75 0 -143 -11 -207 c -15 -95 -72 -125 -117 -125 z"/>
|
||||||
|
<!-- 1: horiz-adv-x="500"-->
|
||||||
|
<path id="one" d="M 89 0 m 205 640 c 0 24 0 26 -23 26 c -62 -64 -150 -64 -182 -64 v -31 c 20 0 79 0 131 26 v -518 c 0 -36 -3 -48 -93 -48 h -32 v -31 c 35 3 122 3 162 3 c 40 0 127 0 162 -3 v 31 h -32 c -90 0 -93 11 -93 48 z"/>
|
||||||
|
<!-- 2: horiz-adv-x="500"-->
|
||||||
|
<path id="two" d="M 50 0 m 399 174 h -25 c -5 -30 -12 -74 -22 -89 c -7 -8 -73 -8 -95 -8 h -180 l 106 103 c 156 138 216 192 216 292 c 0 114 -90 194 -212 194 c -113 0 -187 -92 -187 -181 c 0 -56 50 -56 53 -56 c 17 0 52 12 52 53 c 0 26 -18 52 -53 52 c -8 0 -10 0 -13 -1 c 23 65 77 102 135 102 c 91 0 134 -81 134 -163 c 0 -80 -50 -159 -105 -221 l -192 -214 c -11 -11 -11 -13 -11 -37 h 371 z"/>
|
||||||
|
<!-- 3: horiz-adv-x="500"-->
|
||||||
|
<path id="three" d="M 42 0 m 248 352 c 82 27 140 97 140 176 c 0 82 -88 138 -184 138 c -101 0 -177 -60 -177 -136 c 0 -33 22 -52 51 -52 c 31 0 51 22 51 51 c 0 50 -47 50 -62 50 c 31 49 97 62 133 62 c 41 0 96 -22 96 -112 c 0 -12 -2 -70 -28 -114 c -30 -48 -64 -51 -89 -52 c -8 -1 -32 -3 -39 -3 c -8 -1 -15 -2 -15 -12 c 0 -11 7 -11 24 -11 h 44 c 82 0 119 -68 119 -166 c 0 -136 -69 -165 -113 -165 c -43 0 -118 17 -153 76 c 35 -5 66 17 66 55 c 0 36 -27 56 -56 56 c -24 0 -56 -14 -56 -58 c 0 -91 93 -157 202 -157 c 122 0 213 91 213 193 c 0 82 -63 160 -167 181 z"/>
|
||||||
|
<!-- 4: horiz-adv-x="500"-->
|
||||||
|
<path id="four" d="M 28 0 m 0 165 h 266 v -87 c 0 -36 -2 -47 -76 -47 h -21 v -31 c 41 3 93 3 135 3 c 42 0 95 0 136 -3 v 31 h -21 c -74 0 -76 11 -76 47 v 87 h 100 v 31 h -100 v 455 c 0 20 0 26 -16 26 c -9 0 -12 0 -20 -12 l -307 -469 z M 28 196 m 272 0 h -244 l 244 373 z"/>
|
||||||
|
<!-- 5: horiz-adv-x="500"-->
|
||||||
|
<path id="five" d="M 50 0 m 399 201 c 0 119 -82 219 -190 219 c -48 0 -91 -16 -127 -51 v 195 c 20 -6 53 -13 85 -13 c 123 0 193 91 193 104 c 0 6 -3 11 -10 11 c -1 0 -3 0 -8 -3 c -20 -9 -69 -29 -136 -29 c -40 0 -86 7 -133 28 c -8 3 -10 3 -12 3 c -10 0 -10 -8 -10 -24 v -296 c 0 -18 0 -26 14 -26 c 7 0 9 3 13 9 c 11 16 48 70 129 70 c 52 0 77 -46 85 -64 c 16 -37 18 -76 18 -126 c 0 -35 0 -95 -24 -137 c -24 -39 -61 -65 -107 -65 c -73 0 -130 53 -147 112 c 3 -1 6 -2 17 -2 c 33 0 50 25 50 49 c 0 24 -17 49 -50 49 c -14 0 -49 -7 -49 -53 c 0 -86 69 -183 181 -183 c 116 0 218 96 218 223 z"/>
|
||||||
|
<!-- 6: horiz-adv-x="500"-->
|
||||||
|
<path id="six" d="M 42 0 m 90 328 v 24 c 0 253 124 289 175 289 c 24 0 66 -6 88 -40 c -15 0 -55 0 -55 -45 c 0 -31 24 -46 46 -46 c 16 0 46 9 46 48 c 0 60 -44 108 -127 108 c -128 0 -263 -129 -263 -350 c 0 -267 116 -338 209 -338 c 111 0 206 94 206 226 c 0 127 -89 223 -200 223 c -68 0 -105 -51 -125 -99 z M 132 328 m 119 -322 c -63 0 -93 60 -99 75 c -18 47 -18 127 -18 145 c 0 78 32 178 122 178 c 16 0 62 0 93 -62 c 18 -37 18 -88 18 -137 c 0 -48 0 -98 -17 -134 c -30 -60 -76 -65 -99 -65 z"/>
|
||||||
|
<!-- 7: horiz-adv-x="500"-->
|
||||||
|
<path id="seven" d="M 56 0 m 420 609 c 9 12 9 14 9 35 h -243 c -122 0 -124 13 -128 32 h -25 l -33 -206 h 25 c 3 16 12 79 25 91 c 7 6 85 6 98 6 h 207 c -11 -16 -90 -125 -112 -158 c -90 -135 -123 -274 -123 -376 c 0 -10 0 -55 46 -55 c 46 0 46 45 46 55 v 51 c 0 55 3 110 11 164 c 4 23 18 109 62 171 z"/>
|
||||||
|
<!-- 8: horiz-adv-x="500"-->
|
||||||
|
<path id="eight" d="M 42 0 m 121 457 c -46 30 -50 64 -50 81 c 0 61 65 103 136 103 c 73 0 137 -52 137 -124 c 0 -57 -39 -105 -99 -140 z M 287 377 m 22 -15 c 72 37 121 89 121 155 c 0 92 -89 149 -180 149 c -100 0 -181 -74 -181 -167 c 0 -18 2 -63 44 -110 c 11 -12 48 -37 73 -54 c -58 -29 -144 -85 -144 -184 c 0 -106 102 -173 207 -173 c 113 0 208 83 208 190 c 0 36 -11 81 -49 123 c -19 21 -35 31 -99 71 z M 309 362 m -100 -42 c 28 -17 75 -47 123 -78 c 28 -19 75 -49 75 -110 c 0 -74 -75 -126 -157 -126 c -86 0 -158 62 -158 145 c 0 58 32 122 117 169 z"/>
|
||||||
|
<!-- 9: horiz-adv-x="500"-->
|
||||||
|
<path id="nine" d="M 42 0 m 325 318 v -32 c 0 -234 -104 -280 -162 -280 c -17 0 -71 2 -98 36 c 44 0 52 29 52 46 c 0 31 -24 46 -46 46 c -16 0 -46 -9 -46 -48 c 0 -67 54 -108 139 -108 c 129 0 251 136 251 351 c 0 269 -115 337 -204 337 c -55 0 -104 -18 -147 -63 c -41 -45 -64 -87 -64 -162 c 0 -125 88 -223 200 -223 c 61 0 102 42 125 100 z M 367 318 m -124 -77 c -16 0 -62 0 -93 63 c -18 37 -18 87 -18 136 c 0 54 0 101 21 138 c 27 50 65 63 100 63 c 46 0 79 -34 96 -79 c 12 -32 16 -95 16 -141 c 0 -83 -34 -180 -122 -180 z"/>
|
||||||
|
<!-- .: horiz-adv-x="277.8"-->
|
||||||
|
<path id="dot" d="M 192 378 m 0 -325 c 0 29 -24 53 -53 53 c -29 0 -53 -24 -53 -53 c 0 -29 24 -53 53 -53 c 29 0 53 24 53 53 z"/>
|
||||||
|
</defs>
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
<rect id="background" x="0" y="0" width="600" height="400" fill="none"/>
|
||||||
|
|
||||||
|
<g transform="translate(61.5, 362.5)">
|
||||||
|
<!-- grid -->
|
||||||
|
<g id="grid" transform="scale(1,-1)" style="stroke:black; opacity:0.4; stroke-width:0.5; stroke-linecap:butt">
|
||||||
|
<path id="gridx" d="M 60,0 V 300.5 M 120,0 V 300.5 M 180,0 V 300.5 M 240,0 V 300.5 M 300,0 V 300.5 M 360,0 V 300.5 M 420,0 V 300.5 M 480,0 V 300.5"/>
|
||||||
|
<path id="gridy" d="M 0, 60 H 480 M 0,120 H 480 M 0,180 H 480 M 0,240 H 480 M 0,300 H 480"/>
|
||||||
|
</g>
|
||||||
|
|
||||||
|
<!-- ticks -->
|
||||||
|
<g id="ticks" transform="scale(1,-1)" style="stroke:black; stroke-width:1; stroke-linecap:square">
|
||||||
|
<path id="ticksx" d="M 0,-5 V 5 M 60,-5 V 5 M 120,-5 V 5 M 180,-5 V 5 M 240,-5 V 5 M 300,-5 V 5 M 360,-5 V 5 M 420,-5 V 5 M 480,-5 V 5"/>
|
||||||
|
<path id="ticksy" d="M -5, 0 H 5 M -5, 60 H 5 M -5,120 H 5 M -5,180 H 5 M -5,240 H 5 M -5,300 H 5"/>
|
||||||
|
</g>
|
||||||
|
|
||||||
|
<!-- axes -->
|
||||||
|
<line id="x-axis" x1="0." x2="510.5" y1="0" y2="0" stroke="black" stroke-width="2" stroke-linecap="butt" marker-end="url(#Arrow)"/>
|
||||||
|
<line id="y-axis" x1="0" x2="0" y1="0" y2="-330.5" stroke="black" stroke-width="2" stroke-linecap="butt" marker-end="url(#Arrow)"/>
|
||||||
|
|
||||||
|
<!-- labels -->
|
||||||
|
<g id="chik">
|
||||||
|
<g id="chil" transform="translate(248,-332) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#chi" x="-625.7" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="kchi" transform="translate(248,-332) scale(0.0173,-0.0173)">
|
||||||
|
<use xlink:href="#k" x="0" y="-400"/>
|
||||||
|
</g>
|
||||||
|
<g id="chi2" transform="translate(248,-332) scale(0.0173,-0.0173)">
|
||||||
|
<use xlink:href="#two" x="0" y="600"/>
|
||||||
|
</g>
|
||||||
|
</g>
|
||||||
|
<g id="xl" transform="translate(521,18) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#x" x="-285.75" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="Fkx">
|
||||||
|
<g id="Fx" transform="translate(-3,-340) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#F" x="-2309.6" y="0"/>
|
||||||
|
<use xlink:href="#parleft" x="-1305.6" y="0"/>
|
||||||
|
<use xlink:href="#x" x="-916.7" y="0"/>
|
||||||
|
<use xlink:href="#parright" x="-388.9" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="kF" transform="translate(-3,-340) scale(0.0173,-0.0173)">
|
||||||
|
<use xlink:href="#k" x="-2404.3" y="-200"/>
|
||||||
|
</g>
|
||||||
|
</g>
|
||||||
|
<g id="xlabels" transform="translate(0,29)">
|
||||||
|
<g id="x0" transform="translate(0,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#zero" x="-250" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="x1" transform="translate(60,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#one" x="-250" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="x2" transform="translate(120,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#two" x="-250" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="x3" transform="translate(180,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#three" x="-250" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="x4" transform="translate(240,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#four" x="-250" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="x5" transform="translate(300,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#five" x="-250" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="x6" transform="translate(360,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#six" x="-250" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="x7" transform="translate(420,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#seven" x="-250" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="x8" transform="translate(480,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#eight" x="-250" y="0"/>
|
||||||
|
</g>
|
||||||
|
</g>
|
||||||
|
<g id="ylabels" transform="translate(-11,8)">
|
||||||
|
<g id="y00" transform="translate(0,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#zero" x="-1277.8" y="0"/>
|
||||||
|
<use xlink:href="#dot" x="-777.8" y="0"/>
|
||||||
|
<use xlink:href="#zero" x="-500" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="y02" transform="translate(0,-60) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#zero" x="-1277.8" y="0"/>
|
||||||
|
<use xlink:href="#dot" x="-777.8" y="0"/>
|
||||||
|
<use xlink:href="#two" x="-500" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="y04" transform="translate(0,-120) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#zero" x="-1277.8" y="0"/>
|
||||||
|
<use xlink:href="#dot" x="-777.8" y="0"/>
|
||||||
|
<use xlink:href="#four" x="-500" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="y06" transform="translate(0,-180) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#zero" x="-1277.8" y="0"/>
|
||||||
|
<use xlink:href="#dot" x="-777.8" y="0"/>
|
||||||
|
<use xlink:href="#six" x="-500" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="y08" transform="translate(0,-240) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#zero" x="-1277.8" y="0"/>
|
||||||
|
<use xlink:href="#dot" x="-777.8" y="0"/>
|
||||||
|
<use xlink:href="#eight" x="-500" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="y10" transform="translate(0,-300) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#one" x="-1277.8" y="0"/>
|
||||||
|
<use xlink:href="#dot" x="-777.8" y="0"/>
|
||||||
|
<use xlink:href="#zero" x="-500" y="0"/>
|
||||||
|
</g>
|
||||||
|
</g>
|
||||||
|
|
||||||
|
<!-- the controll points lie on the tangents of the function.
|
||||||
|
they are furthermore positioned in a way to minimize the average
|
||||||
|
quadratic distance between the bezier-curve and the function. -->
|
||||||
|
|
||||||
|
<!-- chi-square distribution curve -->
|
||||||
|
<g transform="scale(60, -60)">
|
||||||
|
<path id="curve-1" fill="none" stroke="#cccc00" stroke-width="0.05px" stroke-linecap="butt" d="M 0.00000,0.00000 C 0.00000,0.69951 0.09236,1.44138 0.30827,2.10627 C 0.48352,2.64596 0.70391,3.02396 0.90274,3.28976 C 1.26413,3.77287 1.71232,4.09619 2.22823,4.32245 C 2.84379,4.59243 3.60266,4.74480 4.55820,4.83619 C 5.43249,4.91982 6.52495,4.95756 8.00000,4.97661"/>
|
||||||
|
<path id="curve-2" fill="none" stroke="#00dd00" stroke-width="0.05px" stroke-linecap="butt" d="M 0.00000,0.00000 C 0.66088,1.65219 1.41027,2.70694 2.28409,3.40417 C 3.01510,3.98746 3.85544,4.33829 4.85611,4.55896 C 5.71844,4.74912 6.73560,4.85053 8.00000,4.90842"/>
|
||||||
|
<path id="curve-3" fill="none" stroke="#00cccc" stroke-width="0.05px" stroke-linecap="butt" d="M 0.00000,0.00000 C 0.00039,0.00000 0.02157,0.00011 0.06577,0.02199 C 0.13607,0.05679 0.21204,0.12022 0.26168,0.16467 C 0.44697,0.33055 0.66992,0.59497 0.91900,0.89580 C 1.28832,1.34184 1.72102,1.87512 2.24855,2.38775 C 2.81740,2.94054 3.43607,3.41058 4.17436,3.78379 C 5.25233,4.32871 6.47631,4.61249 8.00000,4.76994"/>
|
||||||
|
<path id="curve-4" fill="none" stroke="#0000ff" stroke-width="0.05px" stroke-linecap="butt" d="M 0.00000,0.00000 C 0.42114,0.00000 0.88857,0.33244 1.42256,0.79868 C 1.89673,1.21269 2.42571,1.73419 3.04568,2.24895 C 3.61287,2.71989 4.22851,3.16215 4.95182,3.53862 C 5.87028,4.01665 6.85391,4.33219 8.00000,4.54211"/>
|
||||||
|
<!-- <path id="curve-5" fill="none" stroke="#000000"
|
||||||
|
stroke-width="0.05px" stroke-linecap="butt"
|
||||||
|
d="M 0.00000,0.00000
|
||||||
|
C 0.09407,0.00000 0.22013,0.00084 0.36913,0.01931
|
||||||
|
C 0.62912,0.05155 0.90620,0.13086 1.23455,0.29240
|
||||||
|
C 1.79237,0.56683 2.37356,1.01718 3.02976,1.52301
|
||||||
|
C 3.68012,2.02434 4.39005,2.56900 5.23051,3.05800
|
||||||
|
C 6.07454,3.54906 6.96246,3.93292 8.00000,4.21882" />-->
|
||||||
|
<path id="curve-6" fill="none" stroke="#aa00aa" stroke-width="0.05px" stroke-linecap="butt" d="M 0.00000,0.00000 C 0.27785,0.00000 0.58059,0.00006 0.92982,0.05933 C 1.26227,0.11576 1.60114,0.21980 1.98104,0.39283 C 2.48711,0.62333 2.99909,0.94575 3.54987,1.31339 C 4.20194,1.74862 4.89839,2.24040 5.68985,2.70593 C 6.39628,3.12144 7.14459,3.49614 8.00000,3.80948"/>
|
||||||
|
<!-- <path id="curve-7" fill="none" stroke="#000000"
|
||||||
|
stroke-width="0.05px" stroke-linecap="butt"
|
||||||
|
d="M 0.00000,0.00000
|
||||||
|
C 0.23947,0.00000 0.44397,-0.00019 0.64945,0.00653
|
||||||
|
C 1.02199,0.01870 1.40460,0.05400 1.83134,0.15709
|
||||||
|
C 2.28297,0.26618 2.72770,0.43764 3.20850,0.67466
|
||||||
|
C 3.97000,1.05006 4.74882,1.55381 5.61336,2.07226
|
||||||
|
C 6.34119,2.50873 7.11614,2.94734 8.00000,3.33703" />-->
|
||||||
|
<!-- <path id="curve-8" fill="none" stroke="#000000"
|
||||||
|
stroke-width="0.05px" stroke-linecap="butt"
|
||||||
|
d="M 0.00000,0.00000
|
||||||
|
C 0.28449,0.00000 0.48369,-0.00010 0.67310,0.00204
|
||||||
|
C 1.11336,0.00704 1.54213,0.02490 1.99796,0.09463
|
||||||
|
C 2.46863,0.16663 2.93537,0.28900 3.44611,0.48334
|
||||||
|
C 4.07474,0.72255 4.69659,1.04282 5.35484,1.40468
|
||||||
|
C 6.17299,1.85444 7.03211,2.35992 8.00000,2.83265" />-->
|
||||||
|
<path id="curve-9" fill="none" stroke="#ff0000" stroke-width="0.05px" stroke-linecap="butt" d="M 0.00000,0.00000 C 0.44648,-0.00000 0.71567,-0.00017 0.96693,0.00245 C 1.61353,0.00918 2.22202,0.03573 2.87881,0.15547 C 3.51747,0.27190 4.13124,0.46379 4.80065,0.74336 C 5.82505,1.17118 6.85228,1.75096 8.00000,2.32927"/>
|
||||||
|
<!-- <path id="curve-10" fill="none" stroke="#000000"
|
||||||
|
stroke-width="0.05px" stroke-linecap="butt"
|
||||||
|
d="M 0.00000,0.00000
|
||||||
|
C 0.58419,0.00000 0.88886,-0.00014 1.16867,0.00175
|
||||||
|
C 1.84698,0.00634 2.46301,0.02399 3.09782,0.10486
|
||||||
|
C 3.78740,0.19271 4.45162,0.34937 5.18462,0.60746
|
||||||
|
C 6.11333,0.93444 7.02260,1.37844 8.00000,1.85582" />-->
|
||||||
|
</g>
|
||||||
|
|
||||||
|
<g id="legend" transform="translate(397,-214)">
|
||||||
|
<rect id="legend_background" x="0.5" y="0.5" width="120" height="190" fill="white" opacity="0.8"/>
|
||||||
|
<g id="legend_lines" transform="translate(46.5,20)">
|
||||||
|
<path id="curvel-1" transform="translate(0,0)" fill="none" stroke="#cccc00" stroke-width="3px" stroke-linecap="butt" d="M 0,0 H -30"/>
|
||||||
|
<path id="curvel-2" transform="translate(0,30)" fill="none" stroke="#00dd00" stroke-width="3px" stroke-linecap="butt" d="M 0,0 H -30"/>
|
||||||
|
<path id="curvel-3" transform="translate(0,60)" fill="none" stroke="#00cccc" stroke-width="3px" stroke-linecap="butt" d="M 0,0 H -30"/>
|
||||||
|
<path id="curvel-4" transform="translate(0,90)" fill="none" stroke="#0000ff" stroke-width="3px" stroke-linecap="butt" d="M 0,0 H -30"/>
|
||||||
|
<path id="curvel-6" transform="translate(0,120)" fill="none" stroke="#aa00aa" stroke-width="3px" stroke-linecap="butt" d="M 0,0 H -30"/>
|
||||||
|
<path id="curvel-9" transform="translate(0,150)" fill="none" stroke="#ff0000" stroke-width="3px" stroke-linecap="butt" d="M 0,0 H -30"/>
|
||||||
|
</g>
|
||||||
|
<g id="legend_labels" transform="translate(59,26)">
|
||||||
|
<g id="k_is_1" transform="translate(0,0) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#k" x="0" y="0"/>
|
||||||
|
<use xlink:href="#equal" x="581.7" y="0"/>
|
||||||
|
<use xlink:href="#one" x="1420.6" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="k_is_2" transform="translate(0,30) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#k" x="0" y="0"/>
|
||||||
|
<use xlink:href="#equal" x="581.7" y="0"/>
|
||||||
|
<use xlink:href="#two" x="1420.6" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="k_is_3" transform="translate(0,60) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#k" x="0" y="0"/>
|
||||||
|
<use xlink:href="#equal" x="581.7" y="0"/>
|
||||||
|
<use xlink:href="#three" x="1420.6" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="k_is_4" transform="translate(0,90) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#k" x="0" y="0"/>
|
||||||
|
<use xlink:href="#equal" x="581.7" y="0"/>
|
||||||
|
<use xlink:href="#four" x="1420.6" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="k_is_6" transform="translate(0,120) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#k" x="0" y="0"/>
|
||||||
|
<use xlink:href="#equal" x="581.7" y="0"/>
|
||||||
|
<use xlink:href="#six" x="1420.6" y="0"/>
|
||||||
|
</g>
|
||||||
|
<g id="k_is_9" transform="translate(0,150) scale(0.025,-0.025)">
|
||||||
|
<use xlink:href="#k" x="0" y="0"/>
|
||||||
|
<use xlink:href="#equal" x="581.7" y="0"/>
|
||||||
|
<use xlink:href="#nine" x="1420.6" y="0"/>
|
||||||
|
</g>
|
||||||
|
</g>
|
||||||
|
</g>
|
||||||
|
</g>
|
||||||
|
</svg>
|
||||||
|
After 
(image error) Size: 20 KiB |
BIN
notebooks/python/images/Nelder_Mead1.gif
Normal file
BIN
notebooks/python/images/Nelder_Mead1.gif
Normal file
Binary file not shown.
|
After 
(image error) Size: 28 KiB |
BIN
notebooks/python/images/two_hypothsis.png
Normal file
BIN
notebooks/python/images/two_hypothsis.png
Normal file
Binary file not shown.
|
After 
(image error) Size: 80 KiB |
BIN
Теория вероятности/Теория вероятности.pptx
Normal file
BIN
Теория вероятности/Теория вероятности.pptx
Normal file
Binary file not shown.
BIN
Теория оценок/estimates.docx
Normal file
BIN
Теория оценок/estimates.docx
Normal file
Binary file not shown.
66
Теория оценок/estimates.md
Normal file
66
Теория оценок/estimates.md
Normal file
@ -0,0 +1,66 @@
|
|||||||
|
# Понятие о точечной оценке
|
||||||
|
|
||||||
|
Математическая статистика имеет огромное количество разнообразнейших применений, но с точки зрения экспериментальной физики (и как следствие студентов, изучающих эту науку) наиболее интересным применением является оценка параметров закономерностей. Пусть есть некоторое явление природы, которое можно описать при помощи модели $M(\theta)$. Здесь $\theta$ - это некоторый набор параметров модели, которые могут принимать различные значения. На этом этапе мы не оговариваем, как именно модель описывает процесс и что мы можем принимать в качестве параметров. Положим теперь, что существует некоторый выделенный набор параметров $\theta_0$, который соответствует некоторому "истинному" состоянию природы. Далее мы будем исходить из того предположения, что при попытке предпринять некоторые измерения, мы будем получать результаты, соответствующие нашей модели именно с этим набором параметров.
|
||||||
|
|
||||||
|
<div class="note">
|
||||||
|
**Замечание**
|
||||||
|
Тут важно заметить, что мы также негласно предполагаем, что природа вообще действует согласно нашей модели, но этот вопрос мы пока оставим за кадром. В какой-то мере мы вернемся к нему, в главе 5, когда будем обсуждать теорию проверки гипотез.
|
||||||
|
</div>
|
||||||
|
|
||||||
|
Предоставим теперь, что мы провели некоторую серию экспериментов $X = \{X_0, X_1,...X_N\}$, в которых мы тем или иным способом изучаем состояние природы (будем дальше называть результаты этих экспериментов экспериментальной выборкой). Нашей задачей в этой главе будет описание процедуры, при помощи которой можно на основе выборки сделать вывод об истинном состоянии природы $\theta_0$. Важно понимать, что в общем случае, результаты измерений являются случайными величинами, поэтому полученное нами на основании этих данных состояние природы также будет случайной величиной в противовес истинному состоянию природы $\theta_0$, которое вообще говоря, истинно случайной величиной не является. Полученную величину будем называть *точечной оценкой* состояния природы $\hat{\theta}$ или просто оценкой. Саму процедуру, в процессе которой получена оценка, будем называть оцениванием.
|
||||||
|
|
||||||
|
<div class="example">
|
||||||
|
**Пример**
|
||||||
|
Положим, что знания студента в области физики являются состоянием природы (а точнее данного конкретного студента). Очевидно, что досконально проверить этот факт не представляется возможным, поэтому для измерения этой величины мы проводим эксперимент - экзамен. То, что по результатам экзамена оказывается в ведомости является оценкой не только с точки зрения деканата, но и с точки зрения математической статистики.
|
||||||
|
</div>
|
||||||
|
|
||||||
|
В дальнейшем будем считать, что состояния природы описываются действительным числом или набором действительных чисел. Сама по себе теория этого не требует, но в противном случае довольно сложно сравнивать состояния между собой (требуется определять понятие близости в произвольном пространстве). В этом случае наша процедура оценивания:
|
||||||
|
$$
|
||||||
|
\hat{\theta} = f(X)
|
||||||
|
$$
|
||||||
|
является действительной функцией на пространстве векторов $X$, состоящих из случайных переменных. Такие функции еще называют статистиками. Очевидно, что далеко не людая такая функция будет давать тот результат, которого мы хотим. Поэтому вводятся дополнительные обязательные свойства оценок.
|
||||||
|
|
||||||
|
##Свойства точечных оценок
|
||||||
|
|
||||||
|
### Состоятельность
|
||||||
|
Естественное пожелание к оценщику, заключается в том, что качество оценки должно зависеть от объема выборки, числа измерений $n$ случайных переменных $X$: чем больше выборка, тем качественней оценка $\hat{\theta}$. Иными словами, мы хотим, чтобы с ростом объема выборки значение оценки приближалось к истинному значению параметра. При использовании сходимости по вероятности оценку $\hat{\theta}$ определяют как состоятельную, если при любых $\varepsilon > 0$ и $\eta > 0$, найдется такое $N$, что $P \left( \left| \hat{\theta} - \theta \right| \right) < \eta $ при всех $n > N$.
|
||||||
|
|
||||||
|
<div class="note">
|
||||||
|
**Замечание**
|
||||||
|
Нужно заметить, что на практике оценки являются состоятельными только когда при построении оценки не учитывается систематическая ошибка. В противном случае, может наблюдаться сходимость по вероятности не к нулю, а к некоторой фиксированной константе.
|
||||||
|
</div>
|
||||||
|
|
||||||
|
### Несмещенность
|
||||||
|
Рассмотрим набор измерений, каждое из которых состоит из $k$ наблюдений $X$, характеризуемый функцией плотности вероятности $P(\hat\theta | \theta)$ при фиксированном $k$ и определим смещение как отклонение среднего по этому набору $\hat{\theta_k}$ от истинного
|
||||||
|
$$
|
||||||
|
b = E[\hat{\theta_k}] - \theta
|
||||||
|
$$
|
||||||
|
Оценка называется несмещенной, если $b = 0$.
|
||||||
|
|
||||||
|
Заметим, что смещение не зависит от измеренных величин, но зависит от размера образца, формы оценщика и от истинных (в общем случае неизвестных) свойств ФПВ $f(x)$, включая истинное значение параметра. Если смещение исчезает в пределе $n \to \infty$, говорят об асимптотически несмещенной оценке. Заметим, что из состоятельности оценки не следует несмещенность. Это означает, что даже если $\hat{\theta}$ сходится к истинной величине $\theta$ в единичном эксперименте с большим числом измерений, нельзя утверждать, что среднее $\hat{\theta}$ по бесконечному числу повторений эксперимента с конечным числом измерений $n$ будет сходится к истинному $\theta$. Несмещенные оценки пригодны для комбинирования результатов разных экспериментов. В большинстве практических случаев смещение должно быть мало по сравнению со статистической ошибкой и им пренебрегают.
|
||||||
|
|
||||||
|
### Эффективность
|
||||||
|
Для сравнения разных методов оценки, очень важным свойством является эффективность. Говоря простым языком, эффективность - это величина, обратная разбросу значений $\hat{\theta}$ при применении к разным наборам данных. Для того, чтобы хорошо разобраться в этом свойстве, надо вспомнить, что оценка, как случайная величина, распределена с плотностью $P(\hat\theta | \theta)$. Вид этого распределения может быть не известен полностью, но знать его свойства – низшие моменты – необходимо. Среднее по нему суть смещение, а дисперсия $\sigma_{\hat\theta}^2 = \int{ (\hat\theta - \theta} ) P(\hat\theta | \theta) d\hat\theta$ суть мера ошибки в определении оценки. Выбирая между различными методами, мы, естественно, хотим, чтобы ошибка параметра была минимальной из всех доступных нам способов его определения для фиксированного эксперимента. Разные методы обладают разной эффективностью и в общем случае при конечной статистике дисперсия распределения оценки никогда не будет равна нулю. Разумеется, встает вопрос о том, можно ли построить оценку с максимальной возможной эффективностью.
|
||||||
|
|
||||||
|
## Интервальные оценки
|
||||||
|
|
||||||
|
На практике применение точечных оценок сильно затруднено тем, что не известно, на сколько каждая такая оценка точна. Действительно, мы можем спокойно утверждать, что слон весит один килограмм если разброс нашей оценки составляет больше массы слона. Для того, чтобы решить эту проблему есть два пути.
|
||||||
|
Первый путь - это на ряду с точечной оценки указывать меру эффективности этой оценки или ее разброс$\sigma_{\hat\theta}$. Но тут любой внимательный слушатель заметит, что для определения эффективности, вообще говоря, надо знать истинное значение параметра $\theta$, которого мы, разумеется не знаем. Следовательно приходится использовать не эффективность, а оценку этой эффективности, которая сама по себе является случайной величиной. Кроме того, часто случается, что распределение оценки является не симметричным и описать его одним числом не удается.
|
||||||
|
|
||||||
|
Более корректным способом является построение интервальной оценки (доверительного интервала). Формально определение интервальной оценки будет отличаться в зависимости от того, какое определение вероятности вы будете использовать.
|
||||||
|
|
||||||
|
**Частотная интерпретация**: интервальной оценкой параметра или группы параметров $\theta$ с уровнем достоверности $\alpha$ называется такая область на пространстве параметров (в одномерном случае - интервал), которая при многократном повторении эксперимента с вероятностью (частотой) $\alpha$ перекрывает истинное значение $\theta$.
|
||||||
|
|
||||||
|
**Субъективная интерпретация**: доверительным интервалом для параметров $\theta$ будем называть такую область в пространстве параметров, в которой интегральная апостериорная вероятность нахождения истинного значения параметра равна $\alpha$.
|
||||||
|
|
||||||
|
Для точного описания результата проведения анализа как правило в качестве результата приводят как точечную оценку, так и интервальную оценку с некоторым уровнем достоверности (в английском варианте Confidence Level или C. L.). В некоторых случаях приводят несколько интервальных оценок с разным уровнем достоверности. В случае, когда речь идет об определении верхней или нижней границы какого-то параметра, точечная оценка как правило не имеет смысла и в качестве результата дается только интервальная оценка.
|
||||||
|
|
||||||
|
<div class="note">
|
||||||
|
**Замечание**
|
||||||
|
Точечная оценка также не имеет смысла в случае, когда распределение оценки, скажем имеет вид однородного распределения на отрезке. В этом случае все параметры на этом отрезке равновероятны и не понятно, какой из них называть результатом.
|
||||||
|
</div>
|
||||||
|
|
||||||
|
<div class="note">
|
||||||
|
**Замечание**
|
||||||
|
Вполне очевидно, что для одних и тех же данных с использованием одного и того же метода оценивания можно построить бесконечное множество интервальных оценок с фиксированным уровнем достоверности. Действительно, мы можем двигать интервал в разные стороны таким образом, чтобы его вероятностное содержание не менялось. Обычно, если не оговорено иначе, используются так называемые центральные доверительные интервалы, в которых вероятностные содержание за границами интервалов с обеих сторон равны. **Добавить картинку**
|
||||||
|
</div>
|
||||||
BIN
Теория решений/stat.pptx
Normal file
BIN
Теория решений/stat.pptx
Normal file
Binary file not shown.
BIN
Теория решений/vaskin.png
Normal file
BIN
Теория решений/vaskin.png
Normal file
Binary file not shown.
|
After 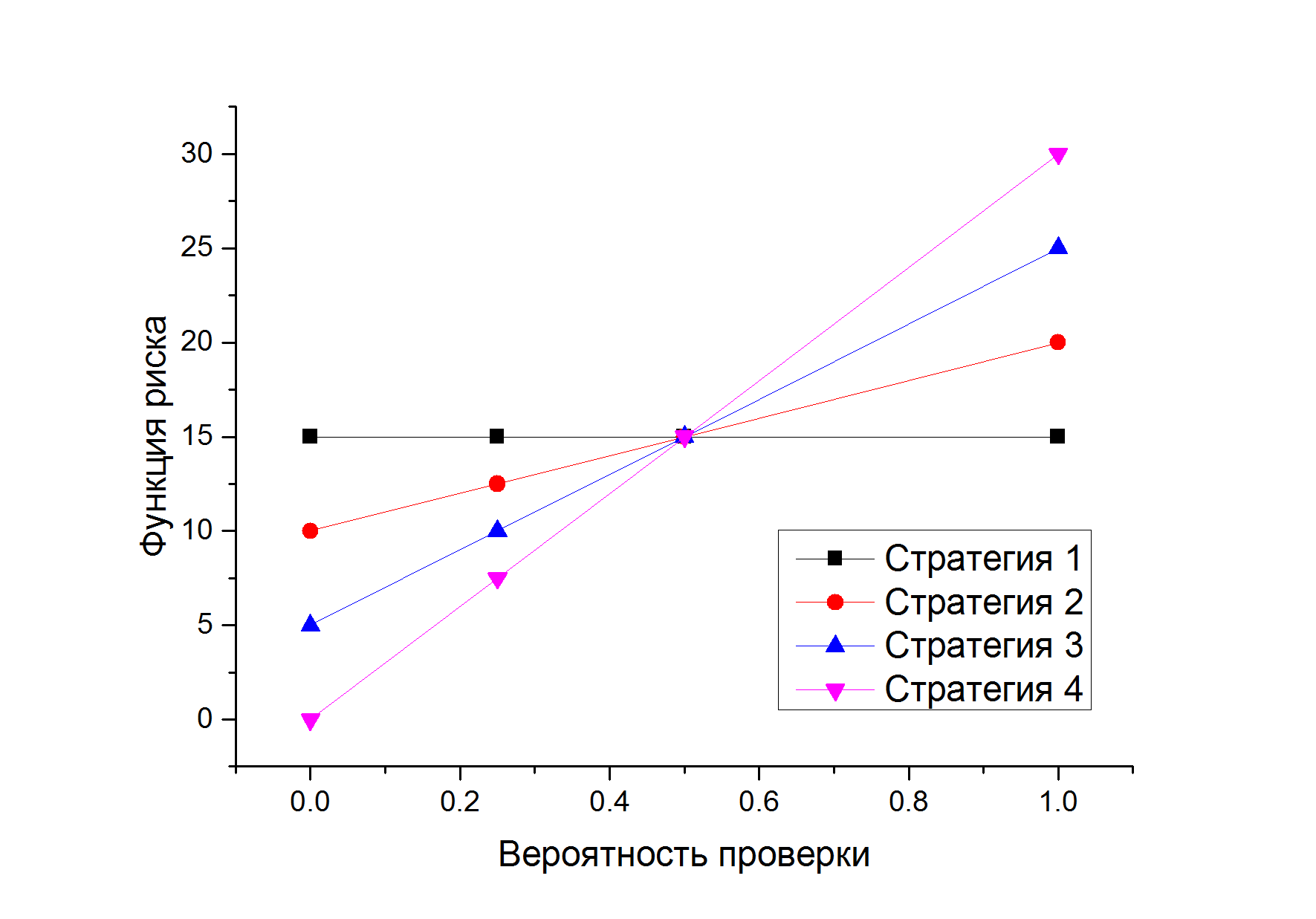
(image error) Size: 26 KiB |
BIN
Теория решений/vaskin1.png
Normal file
BIN
Теория решений/vaskin1.png
Normal file
Binary file not shown.
|
After 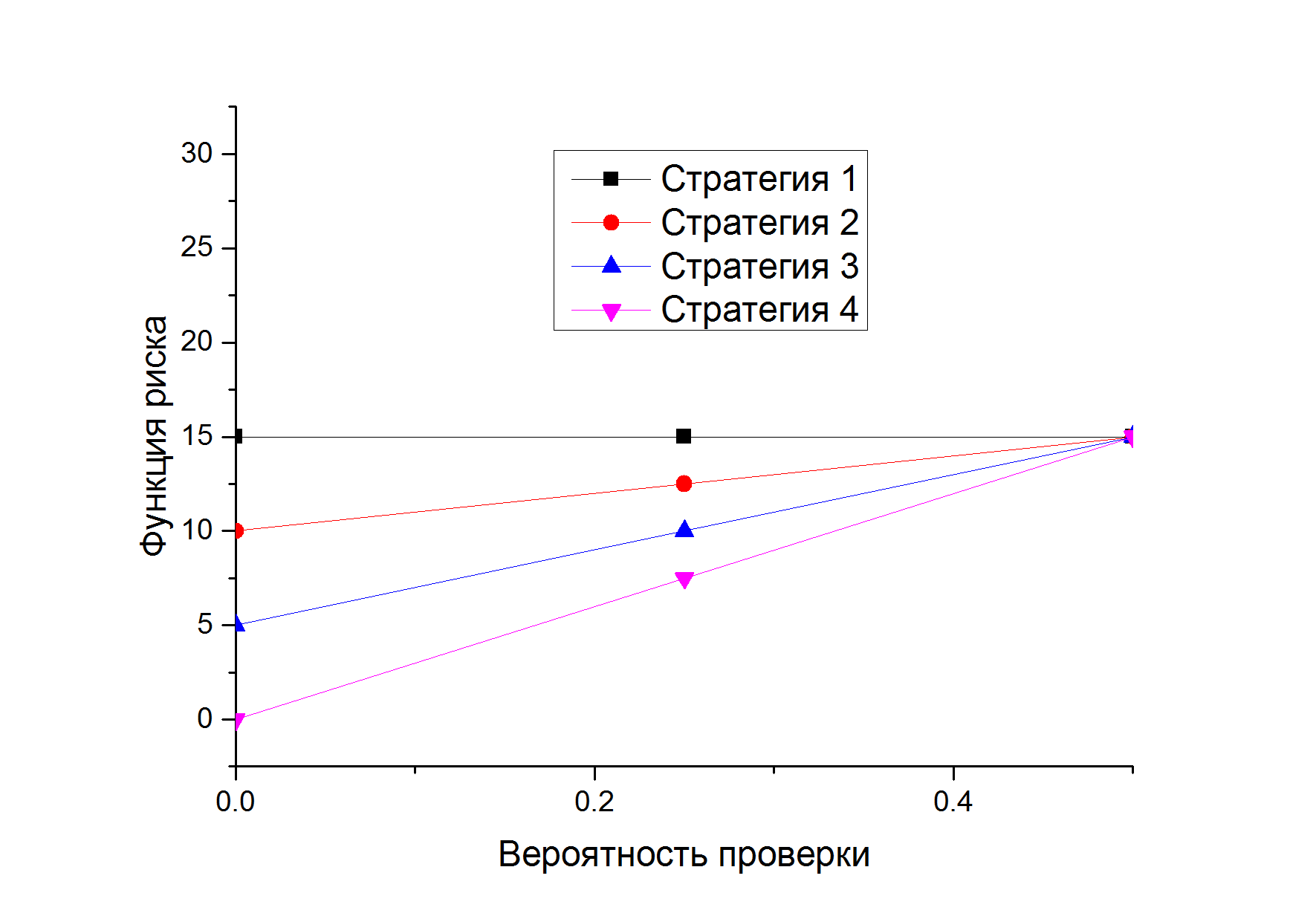
(image error) Size: 24 KiB |
BIN
Теория решений/теория решений.docx
Normal file
BIN
Теория решений/теория решений.docx
Normal file
Binary file not shown.
Loading…
x
Reference in New Issue
Block a user