Interpreters
Results
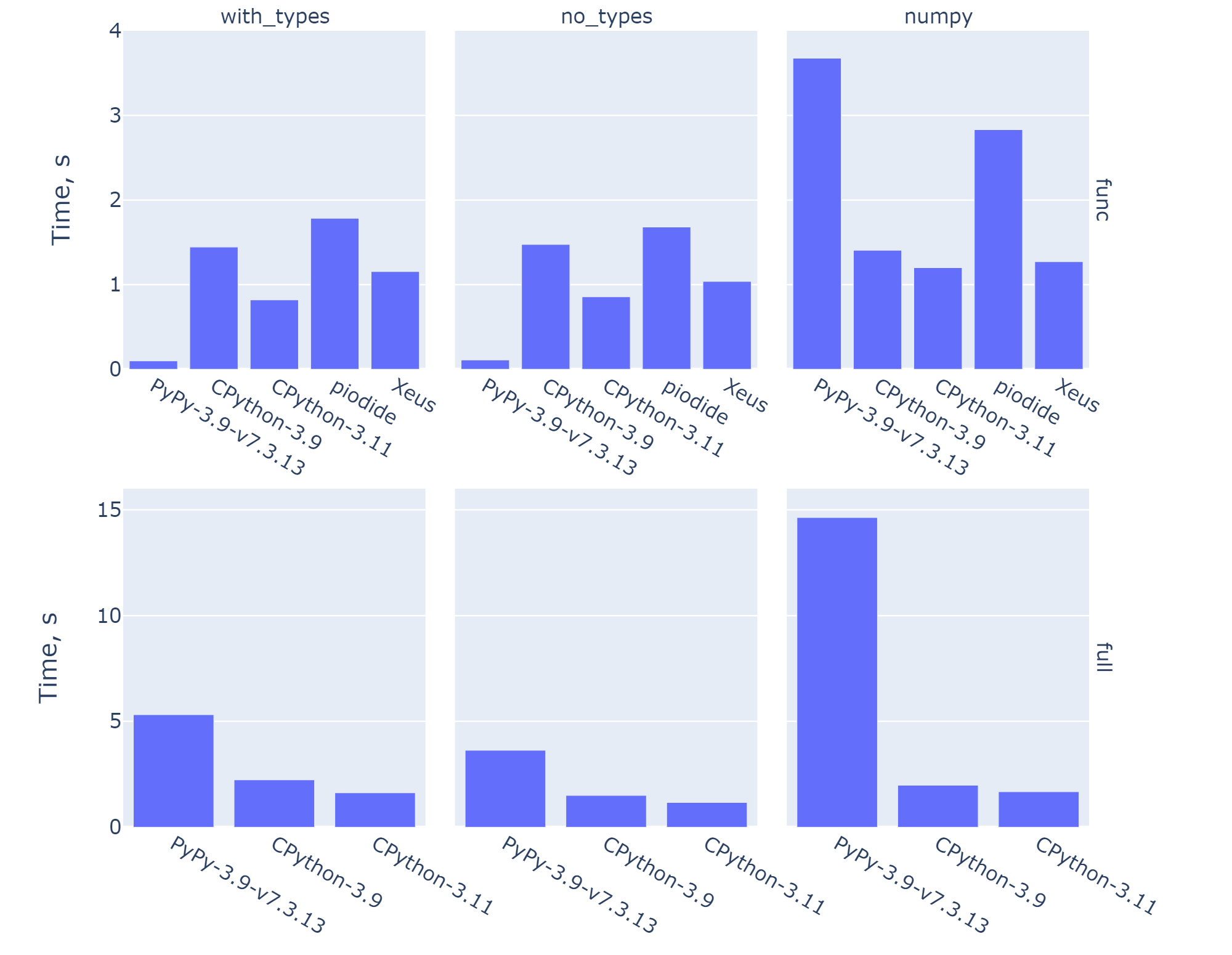
Observations
- Functions w/o Numpy in PyPy run much faster. JIT compilation optimizes the function's code and runs compiled versions of them
\Rightarrow improvement in time
- Entire file evaluation for PyPy takes a bit longer. This may be a drawback of JIT optimization
- PyPy with Numpy is slow. Reason:
- Numpy is written in C
- PyPy's JIT compilation is not compatible with C
- Extra conversion is required (takes time)
- Numpy functions don't give a good improvement in perfomance. Possibly because the code uses classic Python loops instead of numpy vectorisation.
Tested interpreters
- CPython 3.9
- CPython 3.11
- PyPy 3.9 latest
- Pyodide (did not test full file because it only runs in a browser)
- Xeus (again no full file)
Failed to test
- PyPy 3.9 v5.7
- couldn't install numpy
Ignoring ensurepip failure: pip 9.0.1 requires SSL/TLS
- error when testing with types:
invalid syntax --> image: list[list[int]] = [[0 for i in range(qpoints)] for j in range(ppoints)]
- Jython (dependencies issues)
Testing Code
- Tested functions code is in
./test_funcs package
- File for testing function times:
test_func_only.py
- Files for entire evaluation testing:
test_full_{func}.py
- Bash script:
test_full.sh
- Analysis file:
analyse.ipynb
Realisations of mandelbrot functions tested:
def linspace(start, stop, n):
if n == 1:
yield stop
return
h = (stop - start) / (n - 1)
for i in range(n):
yield start + h * i
def mandelbrot_with_types(
pmin: float = -2.5,
pmax: float = 1.5,
qmin: float = -2,
qmax: float = 2,
ppoints: int = 200,
qpoints: int = 200,
max_iterations: int = 300,
infinity_border: float = 100) -> list[list[int]]:
image: list[list[int]] = [[0 for i in range(qpoints)] for j in range(ppoints)]
for ip, p in enumerate(linspace(pmin, pmax, ppoints)):
for iq, q in enumerate(linspace(qmin, qmax, qpoints)):
c: complex = p + 1j * q
z: complex = 0
for k in range(max_iterations):
z = z ** 2 + c
if abs(z) > infinity_border:
image[ip][iq] = 1
break
return image
def mandelbrot_no_types(
pmin=-2.5,
pmax=1.5,
qmin=-2,
qmax=2,
ppoints=200,
qpoints=200,
max_iterations=300,
infinity_border=100):
image = [[0 for i in range(qpoints)] for j in range(ppoints)]
for ip, p in enumerate(linspace(pmin, pmax, ppoints)):
for iq, q in enumerate(linspace(qmin, qmax, qpoints)):
c = p + 1j * q
z = 0
for k in range(max_iterations):
z = z ** 2 + c
if abs(z) > infinity_border:
image[ip][iq] = 1
break
return image
def mandelbrot_np(
pmin=-2.5,
pmax=1.5,
qmin=-2,
qmax=2,
ppoints=200,
qpoints=200,
max_iterations=300,
infinity_border=100):
image = np.zeros((ppoints, qpoints))
for ip, p in enumerate(np.linspace(pmin, pmax, ppoints)):
for iq, q in enumerate(np.linspace(qmin, qmax, qpoints)):
c = p + 1j * q
z = 0
for k in range(max_iterations):
z = z ** 2 + c
if abs(z) > infinity_border:
image[ip, iq] = 1
break
return image
